Sauf que le triomphe ne va pas durer si longtemps que ça, parce que d'autres découvertes un peu plus inattendues vont avoir lieu. Le 28 mars 1802, alors qu'il cherchait à observer Cérès, Heinrich Olbers va tomber sur un autre objet, que l'on baptisera Pallas. L'objet suit une orbite un peu différente de celle de Cérès, mais se situe environ à la même distance du Soleil. Voilà donc une deuxième planète à la place jusque là manquante !

C'est en tout cas comme ça qu'elle est d'abord référencée, mais… on l'observe pendant un certain temps, et elle ne semble pas se rapprocher du Soleil comme les autres comètes. Aucune activité cométaire ne se déclenche. On calcule alors son orbite, et on trouve… un rayon d'un peu moins de 2,8 fois celui de l'orbite terrestre. Soit pile ce qui correspond à la planète manquante dans notre suite mathématique.

Avec cette septième planète découverte par hasard qui se situe pile là où la « loi de Titius-Bode » voulait qu'elle soit, ça semble donc nous indiquer qu'il y a quelque chose à prendre en compte. Et vous avez remarqué comme j'ai mis « Cérès » dans le titre alors qu'on en est maintenant à un tiers du thread et que je ne l'ai juste pas encore évoquée ? On y vient.

Or, en calculant l'orbite de celle-ci, on découvre que son rayon est d'un peu plus de 19 fois celui de l'orbite terrestre. Et (3×2⁶+4)/10 = 19,6. Non seulement la suite mathématique proposée par Titius et Bode correspondait à peu près à l'orbite des planètes connues à l'époque, mais voilà qu'elle semble pouvoir nous prédire également la position d'une planète qu'on ne connaissait pas encore.

Bon, vous qui me lisez du vingt-et-unième siècle ou plus tard (si c'est plus tard : bonjour du passé, j'espère que le Fédivers du futur se porte bien et qu'on ne vous a pas trop pourri la planète à mon époque), vous avez probablement une petite idée de ce qui va suivre. Les gens de la décennie qui a suivi la publication de Bode, en revanche, étaient en droit de se demander « certes, et alors ? », ou quelque chose d'approchant.

Et puis il y a un autre souci : (3×2³+4)/10, ça fait 2,8… ce qui ne correspond pas au rayon de l'orbite de Jupiter. Par contre, (3×2⁴+4)/10, ça fait 5,2, ce qui qui pour le coup correspond parfaitement pour Jupiter. Et (3×2⁵+4)/10 nous donne 10, quand Saturne, dernière des planètes connues à l'époque, est à un peu plus de 9,5 unités astronomique, ce qui a environ l'air de coller aussi. Il faut donc décaler les deux dernières d'un cran. Est-ce qu'il nous manquerait une planète entre Mars et Jupiter ?

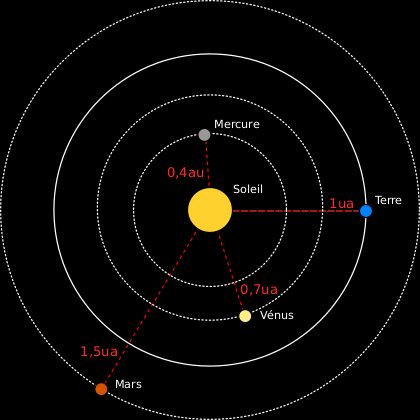
Le terme n'existait pas encore à l'époque, mais Titius a donc remarqué que 1, soit la distance Terre-Soleil, est égal à (3×2¹+4)/10. Bon, ça nous fait une belle jambe. Sauf que Mars est située un peu plus d'une fois et demie plus loin du Soleil que la Terre, donc à une distance d'entre 1,5 et 1,6. Or, 1,6 = (3×2²+4)/10. Et Vénus est pour sa part située à 0,7 unités astronomiques, ce qui est égal à (3×2⁰+4)/10. Il y a quand même une petite ressemblance.
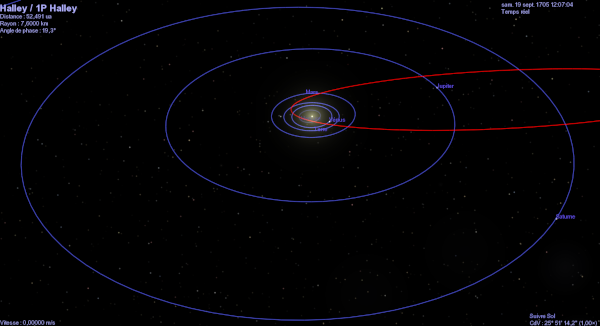
Et effectivement, la comète se présente bien au rendez-vous, prouvant au passage de façon assez magistrale la théorie de la gravitation de Newton (puisque c'est en se basant sur elle que Halley a calculé l'orbite de la comète). Nous savons donc maintenant que les comètes, comme les planètes, font partie de notre système solaire, qui semble donc compter plusieurs sortes de trucs différents. Et c'est quelques années après cette chouette avancée scientifique, plus précisément en 1766, que commence réellement notre histoire.

Edmond Halley change la donne. Il a notamment remarqué, en remontant dans les archives, qu'une de ces comètes semble se manifester tous les 76 ans : un phénomène cyclique, ça laisse donc supposer un objet en orbite, même si celle-ci ne ressemble pas vraiment à celle des planètes. Halley a fait pas mal de calculs pour déterminer cette orbite, et nous prédit donc le retour de cette comète 76 ans après son dernier passage, soit en 1758.
Ah oui, au fait, si vous aviez manqué le thread sur 3I/ATLAS, c'est par là : https://fadrienn.irlnc.org/notice/AwyBqt6c4qOUfKUKjQ
Commençons par nous remettre un peu dans le contexte de l'époque, parce que oui, on replonge ici dans l'Histoire des sciences et dans la découverte de notre système solaire. Depuis les travaux de Copernic, puis de Kepler et de Newton, nous avons compris que (et comment) les planètes tournent autour de notre Soleil. Nous savons aussi, depuis les premières observations de Galilée à la lunette astronomique, qu'il peut y avoir des objets qui tournent autour des planètes, mais ça a longtemps été tout ce qu'on connaissait dans les environs.
En somme :
Les corrélations établies concernant l'adhésion des sciences étudiées à des normes de transparence et de réplicabilité ne sont “statistiquement significatives” que grâce à, à la fois :
1. Un choix de p-value fumeux,
2. Des mesures de politisation douteuses mais arrangeantes.
Au regard de ces mesures arrangeantes :
• Une est reprise telle quelle de la source, bien que peu adaptée à une telle analyse.
• L'autre, par contre, repose sur un choix qui diffère de celui fait dans la source sur la même question. Et sans ce choix différent, pas de “p < 0.10”.
Un des moments cools : vers la fin du parcours, arrivés devant le siège de la communauté de communes, un groupe de jeunes commencent à déployer un drapeau de la Palestine, et les gens autour se mettent spontanément à applaudir.
(Aussi, c'est peut-être parce que mon écran n'est pas assez large, mais le fait qu'il y ait besoin d'ouvrir le menu de navigation à gauche puis cliquer sur le bouton dédié pour voir quelles langues sont dispo n'est pas forcément hyper-pratique, en tout cas ça ne saute pas aux yeux que c'est partiellement traduit quand tu navigues sans savoir.)
Pour les gens chez qui le sondage ne s'affiche pas (ou si ses résultats ne sont pas synchronisés), 67% des gens ont voté pour Cérès et la loi de Bode, qui sera donc le thème du prochain thread.
20% ont voté pour les orchidées de Darwin et 13% pour l'héliocentrisme, donc je me garde ces deux sujets pour en parler une de ces prochaines semaines.
Enfin, personne n'a voté pour la tectonique des plaques, donc je me note de penser à activer les choix multiples sur le prochain sondage, parce que le vote uninominal, quand même, ç'pas terrible.
Ce matin, je siégeais dans un jury RNCP, et pour un des projet, un gars a choisi d'implémenter un LLM localement, pour la souveraineté numérique etc.
Fort bien.
Sa machine n'était pas assez puissante, et il n'a jamais réussi à mettre en prod son site.
C'est tout ce que j'ai à dire.
(Ça va, il n'est jamais connecté à Internet de toute façon, le logiciel qui est dedans se vautre dès qu'on n'est plus sur un réseau local.)
(Si vous voulez tout savoir, c'est un ordi de l'ancien système de projection qu'on a récupéré et adapté pour pouvoir le déplacer sur des événements.)
(Et il fait plus de bruit de ventilo que le vidéoproj' qui est à côté.)
Visiblement, l'habit ne fait pas le moine, mais il fait passer pour le rabbin.
– Mars est sur le bord de la zone habitable, et la ceinture d'astéroïde commence juste après, donc la partie intérieure de la ceinture est vraiment à la limite. D'autant qu'à cette distance, les vents solaires peuvent avoir une influence aussi,
– Une partie des astéroïdes de la ceinture sont des résidus (éventuellement recombinés) d'objets plus lourds qui ont été pulvérisés par des impacts, or les éléments les plus légers sont éjectés plus facilement,
– Les planètes géantes se sont vraisemblablement formées les premières, récupérant une bonne partie de la matière, et les planètes intérieures ont ensuite pris ce qui restait.
Il est fort probable que ces trois points jouent un rôle. Et probablement plusieurs autres auxquels je n'ai pas pensé :-)