Et donc nous voici de nouveau #Vulgadredi, et il va maintenant être temps de consacrer notre #VendrediVulga de la semaine au sujet que vous avez choisi la dernière fois, à savoir : Cérès et la loi de Bode. Ça fait un peu titre de feuilleton, et vous allez voir qu'il y a un peu de quoi. D'ailleurs, ça va nous prendre vingt-quatre pouets.
Commençons par nous remettre un peu dans le contexte de l'époque, parce que oui, on replonge ici dans l'Histoire des sciences et dans la découverte de notre système solaire. Depuis les travaux de Copernic, puis de Kepler et de Newton, nous avons compris que (et comment) les planètes tournent autour de notre Soleil. Nous savons aussi, depuis les premières observations de Galilée à la lunette astronomique, qu'il peut y avoir des objets qui tournent autour des planètes, mais ça a longtemps été tout ce qu'on connaissait dans les environs.
Commençons par nous remettre un peu dans le contexte de l'époque, parce que oui, on replonge ici dans l'Histoire des sciences et dans la découverte de notre système solaire. Depuis les travaux de Copernic, puis de Kepler et de Newton, nous avons compris que (et comment) les planètes tournent autour de notre Soleil. Nous savons aussi, depuis les premières observations de Galilée à la lunette astronomique, qu'il peut y avoir des objets qui tournent autour des planètes, mais ça a longtemps été tout ce qu'on connaissait dans les environs.
2/24 Et puis, j'en avais parlé dans mon thread sur 3I/ATLAS, par un beau jour de 1705 paraît un livre signé Edmond Halley qui se trouve parler de comètes. Les comètes sont un phénomène céleste connus depuis l'antiquité, mais, jusque là, on pensait qu'elles apparaissaient, restaient quelques nuits au dessus de nos têtes, et puis disparaissaient pour de bon, donc personne ne les considérait comme des objets « du système solaire ».
Edmond Halley change la donne. Il a notamment remarqué, en remontant dans les archives, qu'une de ces comètes semble se manifester tous les 76 ans : un phénomène cyclique, ça laisse donc supposer un objet en orbite, même si celle-ci ne ressemble pas vraiment à celle des planètes. Halley a fait pas mal de calculs pour déterminer cette orbite, et nous prédit donc le retour de cette comète 76 ans après son dernier passage, soit en 1758.
Ah oui, au fait, si vous aviez manqué le thread sur 3I/ATLAS, c'est par là : https://fadrienn.irlnc.org/notice/AwyBqt6c4qOUfKUKjQ
Edmond Halley change la donne. Il a notamment remarqué, en remontant dans les archives, qu'une de ces comètes semble se manifester tous les 76 ans : un phénomène cyclique, ça laisse donc supposer un objet en orbite, même si celle-ci ne ressemble pas vraiment à celle des planètes. Halley a fait pas mal de calculs pour déterminer cette orbite, et nous prédit donc le retour de cette comète 76 ans après son dernier passage, soit en 1758.
Ah oui, au fait, si vous aviez manqué le thread sur 3I/ATLAS, c'est par là : https://fadrienn.irlnc.org/notice/AwyBqt6c4qOUfKUKjQ
3/24 En 1758, tout le monde guette donc le retour de cette comète (notamment un certain Charles Messier, mais voyez l'aparté dans l'autre thread). C'est la première fois qu'on s'attend à voir une comète arriver. Mais ce n'est qu'un des exemples assez nombreux en astronomie de cas où on a déterminé un truc sur le papier, et où, ensuite, on attend de voir si on trouve bien ça dans le ciel ou pas.
Et effectivement, la comète se présente bien au rendez-vous, prouvant au passage de façon assez magistrale la théorie de la gravitation de Newton (puisque c'est en se basant sur elle que Halley a calculé l'orbite de la comète). Nous savons donc maintenant que les comètes, comme les planètes, font partie de notre système solaire, qui semble donc compter plusieurs sortes de trucs différents. Et c'est quelques années après cette chouette avancée scientifique, plus précisément en 1766, que commence réellement notre histoire.
Et effectivement, la comète se présente bien au rendez-vous, prouvant au passage de façon assez magistrale la théorie de la gravitation de Newton (puisque c'est en se basant sur elle que Halley a calculé l'orbite de la comète). Nous savons donc maintenant que les comètes, comme les planètes, font partie de notre système solaire, qui semble donc compter plusieurs sortes de trucs différents. Et c'est quelques années après cette chouette avancée scientifique, plus précisément en 1766, que commence réellement notre histoire.

4/24 C'est en effet cette année-là qu'un certain Johann Daniel Titius va publier sur quelque chose d'étrange qu'il a remarqué : il semble y avoir une relation entre les distances au soleil des différentes planètes du système. Il prend pour cela comme unité de base le rayon de l'orbite terrestre, donc la distance entre la Terre et le Soleil. Ce qu'on fait d'ailleurs toujours de nos jours, depuis 1958 on appelle ça une « unité astronomique ».
Le terme n'existait pas encore à l'époque, mais Titius a donc remarqué que 1, soit la distance Terre-Soleil, est égal à (3×2¹+4)/10. Bon, ça nous fait une belle jambe. Sauf que Mars est située un peu plus d'une fois et demie plus loin du Soleil que la Terre, donc à une distance d'entre 1,5 et 1,6. Or, 1,6 = (3×2²+4)/10. Et Vénus est pour sa part située à 0,7 unités astronomiques, ce qui est égal à (3×2⁰+4)/10. Il y a quand même une petite ressemblance.
Le terme n'existait pas encore à l'époque, mais Titius a donc remarqué que 1, soit la distance Terre-Soleil, est égal à (3×2¹+4)/10. Bon, ça nous fait une belle jambe. Sauf que Mars est située un peu plus d'une fois et demie plus loin du Soleil que la Terre, donc à une distance d'entre 1,5 et 1,6. Or, 1,6 = (3×2²+4)/10. Et Vénus est pour sa part située à 0,7 unités astronomiques, ce qui est égal à (3×2⁰+4)/10. Il y a quand même une petite ressemblance.
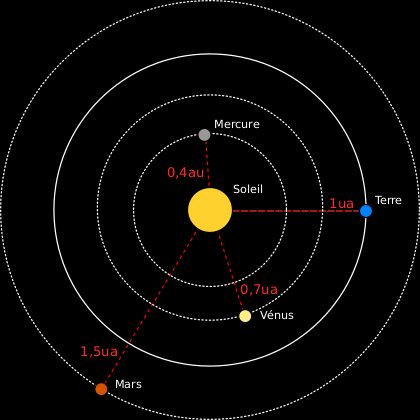
5/24 Bon, ça reste un peu bancal, notamment parce que Vénus n'est pas la première planète du système. Mercure est située à 0,4 unités astronomiques, et pour obtenir ce nombre, il ne faut même pas mettre 2 à la puissance -1, mais carrément à la puissance -∞. On compte peut-être à partir de zéro en informatique, mais il y a quand même peu de cas où on commence à compter à partir de moins l'infini.
Et puis il y a un autre souci : (3×2³+4)/10, ça fait 2,8… ce qui ne correspond pas au rayon de l'orbite de Jupiter. Par contre, (3×2⁴+4)/10, ça fait 5,2, ce qui qui pour le coup correspond parfaitement pour Jupiter. Et (3×2⁵+4)/10 nous donne 10, quand Saturne, dernière des planètes connues à l'époque, est à un peu plus de 9,5 unités astronomique, ce qui a environ l'air de coller aussi. Il faut donc décaler les deux dernières d'un cran. Est-ce qu'il nous manquerait une planète entre Mars et Jupiter ?
Et puis il y a un autre souci : (3×2³+4)/10, ça fait 2,8… ce qui ne correspond pas au rayon de l'orbite de Jupiter. Par contre, (3×2⁴+4)/10, ça fait 5,2, ce qui qui pour le coup correspond parfaitement pour Jupiter. Et (3×2⁵+4)/10 nous donne 10, quand Saturne, dernière des planètes connues à l'époque, est à un peu plus de 9,5 unités astronomique, ce qui a environ l'air de coller aussi. Il faut donc décaler les deux dernières d'un cran. Est-ce qu'il nous manquerait une planète entre Mars et Jupiter ?

6/24 Titius lui-même ne fera pas forcément beaucoup de bruit autour de sa « découverte ». Mais quelques années plus tard, en 1772, Johann Elert Bode publierai à son tour sur le sujet et se débrouillera pour en faire pas mal la publicité, au point qu'on a souvent oublié l'auteur initial pour lui en accorder la paternité. Cette « loi empirique » est donc de nos jours baptisée « loi de Titius-Bode », mais on se contente souvent (comme je l'ai fait moi-même dans le premier pouet et dans le sondage de la semaine dernière) de dire « loi de Bode ».
Bon, vous qui me lisez du vingt-et-unième siècle ou plus tard (si c'est plus tard : bonjour du passé, j'espère que le Fédivers du futur se porte bien et qu'on ne vous a pas trop pourri la planète à mon époque), vous avez probablement une petite idée de ce qui va suivre. Les gens de la décennie qui a suivi la publication de Bode, en revanche, étaient en droit de se demander « certes, et alors ? », ou quelque chose d'approchant.
Bon, vous qui me lisez du vingt-et-unième siècle ou plus tard (si c'est plus tard : bonjour du passé, j'espère que le Fédivers du futur se porte bien et qu'on ne vous a pas trop pourri la planète à mon époque), vous avez probablement une petite idée de ce qui va suivre. Les gens de la décennie qui a suivi la publication de Bode, en revanche, étaient en droit de se demander « certes, et alors ? », ou quelque chose d'approchant.

7/24 Ça ne durera cependant qu'une décennie, parce qu'en 1781, deux astronomes amateurs, William Herschel et sa sœur Caroline, qui, n'ayant pas les moyens de s'acheter un télescope, ont décidé de s'en construire un eux-mêmes, vont faire une découverte assez surprenante en utilisant l'instrument. Ils vont carrément trouver par hasard une planète jusqu'alors inconnue. C'est d'ailleurs Johann Elert Bode qui se chargera de donner à cette nouvelle planète le nom qu'on lui connaît aujourd'hui : Uranus.
Or, en calculant l'orbite de celle-ci, on découvre que son rayon est d'un peu plus de 19 fois celui de l'orbite terrestre. Et (3×2⁶+4)/10 = 19,6. Non seulement la suite mathématique proposée par Titius et Bode correspondait à peu près à l'orbite des planètes connues à l'époque, mais voilà qu'elle semble pouvoir nous prédire également la position d'une planète qu'on ne connaissait pas encore.
Or, en calculant l'orbite de celle-ci, on découvre que son rayon est d'un peu plus de 19 fois celui de l'orbite terrestre. Et (3×2⁶+4)/10 = 19,6. Non seulement la suite mathématique proposée par Titius et Bode correspondait à peu près à l'orbite des planètes connues à l'époque, mais voilà qu'elle semble pouvoir nous prédire également la position d'une planète qu'on ne connaissait pas encore.

- replies
- 1
- announces
- 0
- likes
- 0
8/24 Or, on l'a vu pour la comète de Halley, pouvoir prédire des choses qui se vérifient par la suite, c'est un plutôt très bon signe pour un travail scientifique. En fait, dans tous les cas où on ne peut pas expérimenter pour tester directement nos hypothèses, prédire qu'on devrait observer quelque chose et voir effectivement cette chose arriver, c'est un des meilleurs niveaux de preuve dont on dispose.
Avec cette septième planète découverte par hasard qui se situe pile là où la « loi de Titius-Bode » voulait qu'elle soit, ça semble donc nous indiquer qu'il y a quelque chose à prendre en compte. Et vous avez remarqué comme j'ai mis « Cérès » dans le titre alors qu'on en est maintenant à un tiers du thread et que je ne l'ai juste pas encore évoquée ? On y vient.
Avec cette septième planète découverte par hasard qui se situe pile là où la « loi de Titius-Bode » voulait qu'elle soit, ça semble donc nous indiquer qu'il y a quelque chose à prendre en compte. Et vous avez remarqué comme j'ai mis « Cérès » dans le titre alors qu'on en est maintenant à un tiers du thread et que je ne l'ai juste pas encore évoquée ? On y vient.

9/24 On y vient parce que vingt ans après la découverte des adelphes Herschel, en 1801, le premier janvier pour être précis, un dénommé Giuseppe Piazzi va lui aussi remarquer quelque chose un peu par hasard dans son télescope. Bon, tout le monde n'a pas la chance de découvrir une planète juste comme ça. Piazzi, pour sa part, va penser sur le coup qu'il a fait une découverte devenue entre temps beaucoup plus commune : c'est sans doute une comète.
C'est en tout cas comme ça qu'elle est d'abord référencée, mais… on l'observe pendant un certain temps, et elle ne semble pas se rapprocher du Soleil comme les autres comètes. Aucune activité cométaire ne se déclenche. On calcule alors son orbite, et on trouve… un rayon d'un peu moins de 2,8 fois celui de l'orbite terrestre. Soit pile ce qui correspond à la planète manquante dans notre suite mathématique.
C'est en tout cas comme ça qu'elle est d'abord référencée, mais… on l'observe pendant un certain temps, et elle ne semble pas se rapprocher du Soleil comme les autres comètes. Aucune activité cométaire ne se déclenche. On calcule alors son orbite, et on trouve… un rayon d'un peu moins de 2,8 fois celui de l'orbite terrestre. Soit pile ce qui correspond à la planète manquante dans notre suite mathématique.

10/24 Nouveau triomphe pour la « loi de Titius-Bode », et Bode lui-même va à partir de ce moment faire un lobbying assez intense pour que Cérès, puisque c'est le nom que l'on donne à ce nouvel objet, soit reconnue comme une planète. Après tout, ce n'est manifestement pas une comète, et à cette époque, un objet du système solaire qui n'est pas une comète, c'est forcément une planète, vu qu'on ne connaît encore que ça.
Sauf que le triomphe ne va pas durer si longtemps que ça, parce que d'autres découvertes un peu plus inattendues vont avoir lieu. Le 28 mars 1802, alors qu'il cherchait à observer Cérès, Heinrich Olbers va tomber sur un autre objet, que l'on baptisera Pallas. L'objet suit une orbite un peu différente de celle de Cérès, mais se situe environ à la même distance du Soleil. Voilà donc une deuxième planète à la place jusque là manquante !
Sauf que le triomphe ne va pas durer si longtemps que ça, parce que d'autres découvertes un peu plus inattendues vont avoir lieu. Le 28 mars 1802, alors qu'il cherchait à observer Cérès, Heinrich Olbers va tomber sur un autre objet, que l'on baptisera Pallas. L'objet suit une orbite un peu différente de celle de Cérès, mais se situe environ à la même distance du Soleil. Voilà donc une deuxième planète à la place jusque là manquante !

11/24 Et ce n'est pas fini, car, le premier septembre 1804, Karl Ludwig Harding découvrira Junon. Puis, le 29 mars 1807, fêtant ainsi les cinq ans de sa première découverte, Heinrich Olbers trouvera Vesta dans son télescope. Voici donc quatre nouvelles planètes en relativement peu de temps, portant le total connu à onze… dont quatre sont à la même position dans notre « suite », ce qui est quand même assez étrange.
On décidera par la suite que ça fait un peu trop d'objets à cet endroit, et William Herschel, entre temps devenu astronome professionnel, proposera d'inventer une nouvelle catégorie d'objets pour ranger ces dernières découvertes : ce ne sont pas des comètes, mais pas non plus vraiment des planètes, alors on pourrait les appeler des « astéroïdes » (littéralement, « truc en forme d'astre », parce qu'avec les télescopes de l'époque, ça a l'air d'être juste de petits points brillants, comme les étoiles).
On décidera par la suite que ça fait un peu trop d'objets à cet endroit, et William Herschel, entre temps devenu astronome professionnel, proposera d'inventer une nouvelle catégorie d'objets pour ranger ces dernières découvertes : ce ne sont pas des comètes, mais pas non plus vraiment des planètes, alors on pourrait les appeler des « astéroïdes » (littéralement, « truc en forme d'astre », parce qu'avec les télescopes de l'époque, ça a l'air d'être juste de petits points brillants, comme les étoiles).
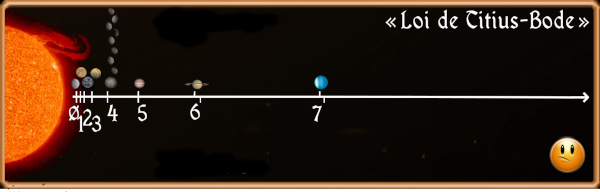
12/24 Herschel propose ce mot (et la nouvelle classification qui l'accompagne) dès 1802, mais il faudra pas mal de temps pour qu'il s'impose. En attendant, et malgré la présence de ces objets supplémentaires, Bode et sa « loi » étaient pris très au sérieux. Après tout, même si le cas de Mercure était toujours un peu étrange, il avait commencé à parler de la possible existence de Cérès bien avant qu'on ne la découvre par accident. Et l'imprévue Uranus semblait elle aussi s'y conforter.
On se disait donc à l'époque que, si l'on devait un jour découvrir encore une planète supplémentaire, celle-ci se trouverait très probablement à la position suivante de la suite mathématique, c'est-à-dire à (3×2⁷+4)/10 = 38,8 unités astronomiques de distance au Soleil. Or, il se trouve qu'on avait précisément des raisons de chercher une planète supplémentaire dans ce coin-là.
On se disait donc à l'époque que, si l'on devait un jour découvrir encore une planète supplémentaire, celle-ci se trouverait très probablement à la position suivante de la suite mathématique, c'est-à-dire à (3×2⁷+4)/10 = 38,8 unités astronomiques de distance au Soleil. Or, il se trouve qu'on avait précisément des raisons de chercher une planète supplémentaire dans ce coin-là.
13/24 En effet, on avait remarqué qu'Uranus ne se comportait pas tout à fait comme on l'attendait : il semblait y avoir un décalage entre la trajectoire calculée d'après les lois de Newton et ce qu'on observait en pratique dans le ciel (c'était aussi le cas pour Mercure, d'ailleurs, mais bon, pour la planète numéro moins l'infini, ça ne faisait qu'une bizarrerie de plus).
Il n'y avait que deux manières d'expliquer ces décalages : soit la théorie de Newton était fausse, ce qui paraissait peu probable après, pour ne parler que de ses vérifications astronomiques, le succès de Halley à propos des comètes… soit il fallait supposer qu'il existait un autre corps céleste, plutôt lourd, situé au delà d'Uranus et qui l'influençait gravitationnellement.
Il n'y avait que deux manières d'expliquer ces décalages : soit la théorie de Newton était fausse, ce qui paraissait peu probable après, pour ne parler que de ses vérifications astronomiques, le succès de Halley à propos des comètes… soit il fallait supposer qu'il existait un autre corps céleste, plutôt lourd, situé au delà d'Uranus et qui l'influençait gravitationnellement.
14/24 Plusieurs personnes se sont donc mises à chercher cette hypothétique planète supplémentaire, avec des télescopes, mais aussi avec une autre sorte d'instrument : du papier et un crayon. En effet, si on peut mesurer les effets gravitationnels de cette planète, on doit pouvoir retrouver l'endroit où elle se trouve par le calcul, non ?
Deux mathématiciens en particulier vont se pencher sur la question : l'anglais John Couch Adams, et le français Urbain Le Verrier. Et tous deux vont se baser sur les lois de Newton, évidemment, nous donnant une idée de la distance de cette nouvelle planète à Uranus ; mais aussi sur la loi de Titius-Bode, qui nous donne sa distance attendue par rapport au Soleil.
Deux mathématiciens en particulier vont se pencher sur la question : l'anglais John Couch Adams, et le français Urbain Le Verrier. Et tous deux vont se baser sur les lois de Newton, évidemment, nous donnant une idée de la distance de cette nouvelle planète à Uranus ; mais aussi sur la loi de Titius-Bode, qui nous donne sa distance attendue par rapport au Soleil.
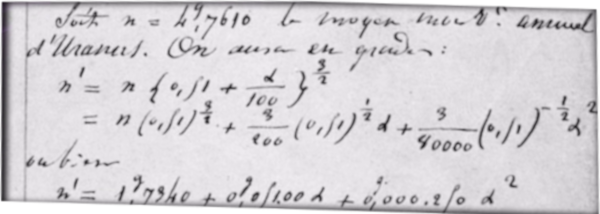
15/24 Tous deux travaillent indépendamment l'un de l'autre, et Adams est le premier à obtenir un résultat. Début août 1846, il transmet les coordonnées qu'il a calculées à James Challis, directeur de l'observatoire de Cambridge, qui pointe son meilleur télescope… et ne trouve rien. Il s'avérera par la suite, après vérification, que Challis a bel et bien observé Neptune à plusieurs reprises à cette période, mais que, les cartes du ciel sur lesquels il se basait n'étant pas à jour, il n'a pas réussi à différencier la planète des étoiles situées aux alentours.
Entre temps, Le Verrier sera lui aussi arrivé à un résultat, qu'il transmettra à Johann Gottfried Galle, de l'observatoire de Berlin, lequel parviendra à localiser cette nouvelle planète dans son télescope le 23 septembre de la même année. C'est donc au mathématicien français qu'est attribuée la découverte de cette nouvelle planète, que l'on baptisera par la suite Neptune.
Pour plus de détails sur ces péripéties-là, voyez ici : https://fr.wikipedia.org/wiki/D%C3%A9couverte_de_Neptune
Entre temps, Le Verrier sera lui aussi arrivé à un résultat, qu'il transmettra à Johann Gottfried Galle, de l'observatoire de Berlin, lequel parviendra à localiser cette nouvelle planète dans son télescope le 23 septembre de la même année. C'est donc au mathématicien français qu'est attribuée la découverte de cette nouvelle planète, que l'on baptisera par la suite Neptune.
Pour plus de détails sur ces péripéties-là, voyez ici : https://fr.wikipedia.org/wiki/D%C3%A9couverte_de_Neptune
16/24 (Pour la petite histoire, peu après avoir été crédité de la découverte de cette nouvelle planète, Le Verrier aurait déclaré que, quand même, ça aurait été mieux si on avait baptisée Uranus du nom de William Herschel. Je vous laisse interpréter vous-mêmes les implications de cette déclaration.)
Voilà en tout cas une nouvelle confirmation éclatante des lois de Newton et de Bode, la planète étant précisément là où on l'attendait. Ou peut-être pas ? À partir des premières observations, on repère le trajet de cette planète dans le ciel, et on calcule donc plus précisément sa trajectoire… et l'on se rend compte qu'elle n'est située qu'à 30 unités astronomiques du Soleil, et pas du tout 38,8. Oups.
Voilà en tout cas une nouvelle confirmation éclatante des lois de Newton et de Bode, la planète étant précisément là où on l'attendait. Ou peut-être pas ? À partir des premières observations, on repère le trajet de cette planète dans le ciel, et on calcule donc plus précisément sa trajectoire… et l'on se rend compte qu'elle n'est située qu'à 30 unités astronomiques du Soleil, et pas du tout 38,8. Oups.

17/24 Les lois de Newton ne sont pas spécialement affectées par ce décalage, car après tout, Adams et Le Verrier ont travaillé avec des incertitudes et des valeurs approchées, et la position reste à ce niveau cohérente avec ce qu'on attendait (et reste donc une bonne confirmation de ce côté). Mais c'est par contre une réfutation franche et nette de la « loi de Titius-Bode », puisque là, clairement, rien ne correspond.
Le fait que les orbites des planètes jusqu'à Uranus correspondent à peu près à ce que nous disait cette « loi » n'était qu'un simple hasard, et (3×2ⁿ+4)/10 n'a en fait aucune signification particulière. Ce qui devrait nous rappeler que, malgré tout, on peut quand même avoir raison plusieurs fois par pur hasard, et qu'il vaut donc mieux ne pas trop se monter la tête.
Le fait que les orbites des planètes jusqu'à Uranus correspondent à peu près à ce que nous disait cette « loi » n'était qu'un simple hasard, et (3×2ⁿ+4)/10 n'a en fait aucune signification particulière. Ce qui devrait nous rappeler que, malgré tout, on peut quand même avoir raison plusieurs fois par pur hasard, et qu'il vaut donc mieux ne pas trop se monter la tête.
18/24 Oublions donc la loi de Titius-Bode et revenons en à Cérès, sur laquelle il reste quelques trucs intéressants à dire. D'abord, on peut noter que peu avant la découverte de Neptune, le 8 décembre 1845, un cinquième astéroïde avait été découvert, baptisé Astrée. À partir de l'année 1847, on se mettra à en trouver de plus en plus, au moins un part an. Plus encore depuis que nos moyens d'observation se sont considérablement améliorés : on connaît maintenant quelques centaines de milliers d'astéroïdes.
Cérès ne sera donc pas restée rangée parmi les planètes tellement plus longtemps qu'elle n'a été rangée parmi les comètes. Mais il se trouve qu'elle ne restera pas non plus éternellement dans la case des astéroïdes. Son statut va de nouveau changer à partir de 2006, des suites (un peu tardives) de la découverte d'encore un autre objet du système solaire : Pluton.
Cérès ne sera donc pas restée rangée parmi les planètes tellement plus longtemps qu'elle n'a été rangée parmi les comètes. Mais il se trouve qu'elle ne restera pas non plus éternellement dans la case des astéroïdes. Son statut va de nouveau changer à partir de 2006, des suites (un peu tardives) de la découverte d'encore un autre objet du système solaire : Pluton.

19/24 Je ne vais pas détailler cette découverte-ci, ça ferait un thread un peu long… et surtout je l'ai déjà fait dans une vidéo que je vous conseille donc d'aller regarder en complément. Une partie de ce que j'y raconte est commun avec ce qu'on vient de voir, mais je n'insiste pas sur les mêmes éléments (je fais complètement l'impasse sur les comètes, et Titius et Bode ne sont pas mentionnés à l'oral ; par contre j'y parle un peu plus des étrangetés de l'orbite de Mercure et des critères du nouveau classement, entre autres).
Mais donc, après la découverte de Pluton en 1930, l'astronome néerlandais Gerard Kuiper suggérera en 1951 que celle-ci fait partie d'une deuxième ceinture d'astéroïdes, et il faudra de nouveau un peu de patience avant la confirmation puisqu'on ne commencera à découvrir ses voisins que plus de quarante ans plus tard, en 1992. Et encore quatorze ans plus tard, on décidera, comme pour Cérès et les premiers astéroïdes, de ne plus compter Pluton comme une planète, mais d'inventer une nouvelle catégorie : celle des planètes naines.
Pour plus de détails, la vidéo : https://skeptikon.fr/w/47e8f219-4bf5-4b06-ad76-4f6fcc499d03
Mais donc, après la découverte de Pluton en 1930, l'astronome néerlandais Gerard Kuiper suggérera en 1951 que celle-ci fait partie d'une deuxième ceinture d'astéroïdes, et il faudra de nouveau un peu de patience avant la confirmation puisqu'on ne commencera à découvrir ses voisins que plus de quarante ans plus tard, en 1992. Et encore quatorze ans plus tard, on décidera, comme pour Cérès et les premiers astéroïdes, de ne plus compter Pluton comme une planète, mais d'inventer une nouvelle catégorie : celle des planètes naines.
Pour plus de détails, la vidéo : https://skeptikon.fr/w/47e8f219-4bf5-4b06-ad76-4f6fcc499d03
20/24 Quelle est la différence entre une planète naine et un astéroïde ? La masse. Quoique beaucoup moins massive qu'une planète, Pluton l'est quand même suffisamment pour que la gravité l'oblige à prendre une forme globalement sphérique, tandis que les astéroïdes, dont la masse est encore beaucoup plus faible, ont des formes beaucoup plus variées.
Et, vous l'aurez vu venir : on s'est entre temps rendu compte que Cérès, avec ses ≃10¹⁸ tonnes (soit un tiers de la masse totale de la ceinture d'astéroïdes à elle seule), est suffisamment massive pour être dans le même cas. On la considère donc maintenant comme une planète naine, au même titre que Pluton et quelques autres. Ce qui fait qu'on l'a rangée dans chacune des quatre catégories d'objet du système solaire à mesure qu'on les inventait. Encore une fois, un bon rappel du fait que notre façon de ranger peut pas mal varier avec le temps.
Et, vous l'aurez vu venir : on s'est entre temps rendu compte que Cérès, avec ses ≃10¹⁸ tonnes (soit un tiers de la masse totale de la ceinture d'astéroïdes à elle seule), est suffisamment massive pour être dans le même cas. On la considère donc maintenant comme une planète naine, au même titre que Pluton et quelques autres. Ce qui fait qu'on l'a rangée dans chacune des quatre catégories d'objet du système solaire à mesure qu'on les inventait. Encore une fois, un bon rappel du fait que notre façon de ranger peut pas mal varier avec le temps.
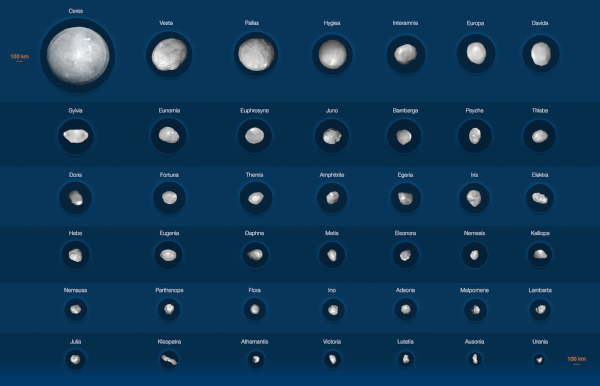
21/24 Cérès est donc à ce jour la plus petite des planètes naines connues, mais aussi la plus proche de nous, puisque les autres sont dans la lointaine ceinture de Kuiper avec Pluton (voire encore au delà). Comme la ceinture principale n'est pas « si loin que ça », on a décidé d'aller voir : la sonde Dawn, lancée en 2007, après être passée à proximité de Mars, puis avoir tourné autour de Vesta à partir de 2011, s'est mise en orbite autour de Cérès en 2015, où elle est restée en activité jusqu'en 2018.
Ses premiers résultats ont peut-être été un peu éclipsés par ceux de New Horizons, une sonde partie l'année précédente, en 2006, et qui, profitant d'une configuration favorable, a pu foncer assez vite pour atteindre Pluton en « seulement » neuf ans de voyage, et nous envoyer les premiers clichés deux mois après l'arrivée de Dawn à proximité de Cérès ; mais, pour les résultats de New Horizons, voyez ma vidéo sur Pluton.
Ses premiers résultats ont peut-être été un peu éclipsés par ceux de New Horizons, une sonde partie l'année précédente, en 2006, et qui, profitant d'une configuration favorable, a pu foncer assez vite pour atteindre Pluton en « seulement » neuf ans de voyage, et nous envoyer les premiers clichés deux mois après l'arrivée de Dawn à proximité de Cérès ; mais, pour les résultats de New Horizons, voyez ma vidéo sur Pluton.
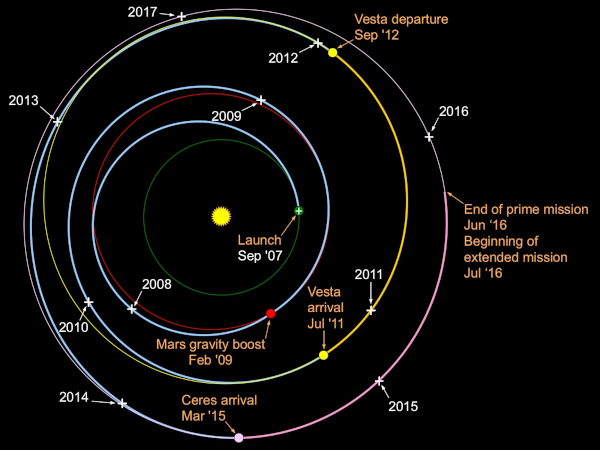
22/24 Parlons donc davantage de ceux de Dawn. On a notamment pu se rendre compte que la première intuition de Giuseppe Piazzi, même s'il n'avait pas encore toutes ces infos, n'était pas forcément si mauvaise, car Cérès semble finalement avoir un certain nombre de points communs avec les comètes : elle est composée de roche, mais également de glace, et on y a détecté de la matière organique (comme les acides aminés dans les comètes, mais je n'ai pas ici les détails de ce dont il s'agit précisément).
Comme les comètes (c'est de là que vient leur nom, cf. le thread sus-mentionné), Cérès possède même une « chevelure » : une atmosphère très fine composée en grande partie de vapeur d'eau, en l'occurrence alimentée par des geysers. Son histoire est peut-être aussi assez similaire à celle des comètes : les observations semblent indiquer que Cérès a pu se former dans la ceinture de Kuiper ou au delà, avant que les jeux de billard cosmique ne l'amènent à sa position actuelle.
Comme les comètes (c'est de là que vient leur nom, cf. le thread sus-mentionné), Cérès possède même une « chevelure » : une atmosphère très fine composée en grande partie de vapeur d'eau, en l'occurrence alimentée par des geysers. Son histoire est peut-être aussi assez similaire à celle des comètes : les observations semblent indiquer que Cérès a pu se former dans la ceinture de Kuiper ou au delà, avant que les jeux de billard cosmique ne l'amènent à sa position actuelle.

23/24 On a pu déterminer que Cérès possède une structure différenciée, avec un noyau fait de roche et un manteau fait de glace. Il n'est pas impossible que, comme Europe ou Ganymède, elle possède un océan d'eau liquide situé sous la couche de glace. Pas assuré, cependant, car si elle a sans doute eu une activité interne par le passé, avec notamment un volcanisme d'eau, elle s'est rapidement refroidie, et ce qui lui reste d'activité aujourd'hui semble uniquement dû aux impacts par des corps environnants.
Ça reste néanmoins un objet particulièrement intéressant à étudier, aussi intéressant par ses caractéristiques propres que l'histoire de sa découverte et de son classement est riche en rebondissements. Malgré quelques siècles de télescope, nous sommes encore loin de tout connaître sur notre système solaire.
Ça reste néanmoins un objet particulièrement intéressant à étudier, aussi intéressant par ses caractéristiques propres que l'histoire de sa découverte et de son classement est riche en rebondissements. Malgré quelques siècles de télescope, nous sommes encore loin de tout connaître sur notre système solaire.

24/24 Donc voilà, ça méritait bien un thread pas si petit que ça pour en parler, mais bon, je bosse ce week-end, donc j'étais de repos aujourd'hui (et j'ai profité de la grève hier pour en écrire un bon bout). Puis j'avais dû sabrer pas mal de choses dans la vidéo sur Pluton pour que ça tienne en une demi-heure (à la base, c'était une séance de planétarium, donc il y avait des contraintes), donc ça méritait bien un petit complément.
On essayera de revenir à un thread plus court la prochaine fois. Qui a des chances de porter sur l'évolution vu les résultats du dernier sondage, mais si vous avez des suggestions ou si j'ai une autre idée entre temps, on verra bien ! En attendant, merci pour la lecture, j'espère que ça continue de vous plaire. N'hésitez pas à me faire des retours :-)
En attendant, si vous avez loupé le thread de la semaine dernière, c'est par là : https://fadrienn.irlnc.org/notice/Ay8UtAQpuelCbeADui
On essayera de revenir à un thread plus court la prochaine fois. Qui a des chances de porter sur l'évolution vu les résultats du dernier sondage, mais si vous avez des suggestions ou si j'ai une autre idée entre temps, on verra bien ! En attendant, merci pour la lecture, j'espère que ça continue de vous plaire. N'hésitez pas à me faire des retours :-)
En attendant, si vous avez loupé le thread de la semaine dernière, c'est par là : https://fadrienn.irlnc.org/notice/Ay8UtAQpuelCbeADui
@elzen
Merci, c'est passionnant ! 🤩
Oui, moi j'ai une suggestion pour le prochain thread : la lune est-elle une banane, et si oui où est l'épluchure ?
(bonus si tu as la ref)
Ou sinon, la lune est-elle un oeuf, et si oui quand va-t'il éclore ?