Le Livre d'Argent

Nous sommes de nouveau #VendrediVulga, et mine de rien, ça fait quand même cinq mois qu'il y a un #Vulgadredi par semaine, je suis plutôt content de moi ! Dans ces threads, on a parlé un peu de la vie et pas mal de l'univers… mais on ne va pas attendre le quarante-deuxième épisode pour commencer à parler du reste. Donc, il est temps de consacrer seize pouets à notre façon de compter.

Compter, c'est quelque chose qu'on fait depuis très longtemps. D'ailleurs, les plus anciennes traces d'écriture qu'on ait retrouvées, datées d'il y a cinq mille ans et quelques siècles, semblent avoir été dédiées à compter les possessions des gens de l'époque, avant que le système ne se développe et devienne ce qu'on appelle aujourd'hui le cunéiforme.

2/16 J'ai mentionné dans un thread précédent qu'on avait inventé l'agriculture plusieurs fois, à des lieux et des millénaires différents. Ce n'est pas la seule chose dans ce cas, puisque, beaucoup plus proches de nous dans le temps et sans lien avec l'écriture mésopotamienne, les civilisations andines utilisaient de leur côté des cordelettes nouées appelées quipus.

Il semble que ces quipus aient été utilisées comme une forme d'écriture permettant de transmettre des messages sur de longues distances, même si, là encore, leur usage premier et principal était de compter des choses. Et si le sujet de l'écriture est super intéressant, c'est sur ce point-ci, le comptage, qu'on va donc se concentrer ici.

3/16 Dans le thread de la semaine dernière, j'ai mentionné le système international d'unités, et précisé qu'il était généralement plus pratique à utiliser que ses concurrents. Une des raisons à ça, c'est son côté régulier : là où un pied mesure douze pouces, et où une livre pèse seize onces, on passe d'une subdivision à l'autre des unités du système international uniquement par des multiples de dix.

Un mètre mesure cent centimètres, et un kilogramme pèse mille gramme, c'est simple et ça évite de jongler entre plein de multiplications complexes (en tout cas pour nous qui maîtrisons à peu près le concept de nombres à virgules). On peut quand même noter une petite bizarrerie pour les poids, puisque c'est le kilogramme et pas le gramme qui sert d'unité de base officielle, mais bon.

Dans tous les cas, ce qui compte est que les unités de base soient des grandeurs pratiques pour nous… encore que ça dépende de ce qu'on cherche à mesurer, mais, donc, voyez là : https://fadrienn.irlnc.org/notice/B1BJ6BmZj213zACWhs

4/16 Mais pourquoi est-ce que c'est plus pratique ? Parce que, dans notre vie de tous les jours, nous comptons principalement « en base dix », avec un système « décimal ». Ça se voit plutôt bien à notre façon à nous d'écrire les nombres, avec des combinaisons de chiffres de zéro à neuf.

Même si ça n'a pas toujours été le cas, ce qui a laissé quelques traces dans notre façon de parler (le fameux « quatre-vingt-dix » par exemple), nous sommes tellement habitué·e·s à regrouper les nombres par paquets de dix, puis de cent, puis de mille, etc., que ça nous demande moins de réflexion que de faire des multiplications et divisions par n'importe quoi d'autre.

Mais on pourrait, en pratique, compter très différemment, comme le font par exemple les Shadoks : https://tube-maternelle.apps.education.fr/w/0390e429-0aad-49e1-ba68-64e5b95a2aec

5/16 Si j'aime beaucoup la vidéo sus-mentionnée, on peut aussi prendre d'autres exemples. Tiens, vu que le premier thread, il y a cinq mois, partait d'un très chouette jeu vidéo, on va revenir à ce thème en parlant d'un autre excellent jeu : Riven, le deuxième opus de la saga Myst (ce qui me permet au passage de remercier @defakator, vu que c'est en réaction à ses lives de jeux que cette série de threads est partie et que, justement, Riven est le dernier jeu qu'il a terminé au moment où j'écris ça).

Dans Riven, donc, nous avons pour tâche d'explorer une île peuplée d'habitant·e·s un brin fuyant·e·s qui parlent une langue assez différente de la nôtre. Si nous avons la chance de tomber de temps en temps sur des journaux écrits en français (ou en anglais en V.O.) qui nous permettent de de découvrir pas mal de choses sur l'histoire, on trouve tout de même des séries de symboles étranges qu'il nous faudra apprendre à déchiffrer.

6/16 « En effet, il y a deux sortes de jeux vidéos ». Ceux dans lesquels notre personnage apprend des techniques qu'on pourra ensuite réutiliser en appuyant sur un bouton, et ceux dans lesquels c'est le joueur ou la joueuse qui doit apprendre des choses pour pouvoir progresser. Riven est dans cette seconde catégorie, et nous amènera pour cela carrément dans une salle de classe.

Là, un dispositif intriguant nous permet de comprendre peu à peu que ces symboles étranges sont en fait des séries de chiffres. Mais avec un système de numération un peu différent du nôtre : il n'y a que cinq chiffres, qui peuvent être retournés et combinés deux par deux pour former vingt-cinq nombres différents, ce qui est amplement suffisant pour nos besoins dans le jeu.

7/16 On nous répète à plusieurs reprises que le nombre cinq est très important pour les habitant·e·s de Riven : c'est tellement vrai que leur système de numération fonctionne en base cinq, et non pas en base dix comme le nôtre. Et c'est quelque chose qu'on peut réussir à comprendre juste en utilisant un petit jouet éducatif en bois, ce qui est quand même sacrément cool.

On n'apprend pas suffisamment sur la civilisation rivenienne dans le jeu pour connaître jusqu'à leur système d'unités, mais il a donc peu de chances d'être le même que notre système international, dont les opérations doivent leur paraître un brin complexes, puisque leur système entraîne probablement des habitudes de comptage assez différentes.

8/16 Évidemment, Riven n'est qu'un jeu vidéo et ses habitant·e·s n'existent pas. Mais pour faire tourner ce jeu vidéo, nous avons besoin d'ordinateurs, et eux non plus ne comptent pas exactement comme nous : ces machines, fondamentalement, ne savent gérer que des séquences de zéros et de uns, ce qui pour elles correspond à la présence ou l'absence de courant à la sortie d'un composant électronique.

Bien sûr, ces différentes séquences de zéros et de uns sont interprétés de façon à faire en sorte que nos machines affichent des images, jouent du son, ou bien encore génèrent du baratin, mais fondamentalement, un ordinateur est encore une fois une grosse machine à compter, mais avec un nombre de chiffres différents assez limité.

Tenez, @gee donnait un peu plus de détails ici, par exemple : https://grisebouille.net/des-zeros-et-des-uns/

9/16 Pour les étudiant·e·s en première année d'informatique, donc, certains cours consistent à… apprendre à compter. Et notamment à poser des opérations « à la main », exactement comme on a appris à le faire en primaire, mais en utilisant le binaire plutôt que le décimal.

Quand je donnais des cours à la fac, c'était souvent une occasion pour moi d'indiquer aux étudiant·e·s que j'avais été prof d'écoles avant d'arriver devant elleux et qu'il n'y avait pas de raison qu'iels s'en sortent moins bien que mes élèves de l'époque, vu que le principe est grosso-modo le même.

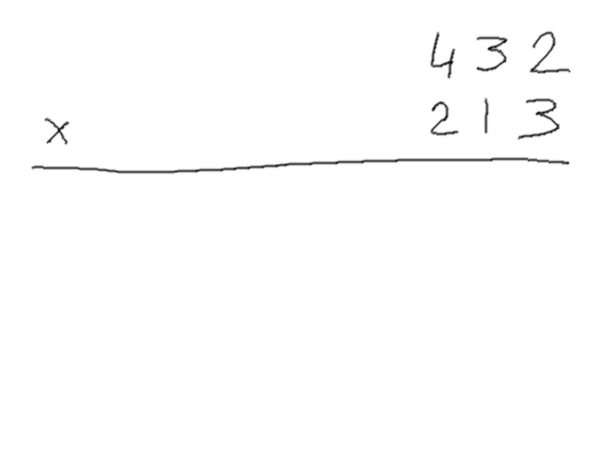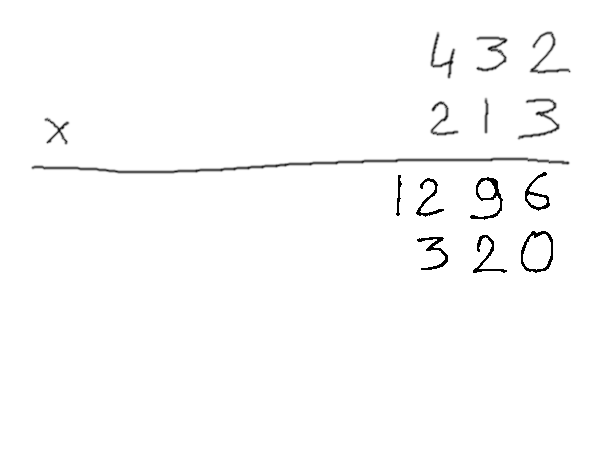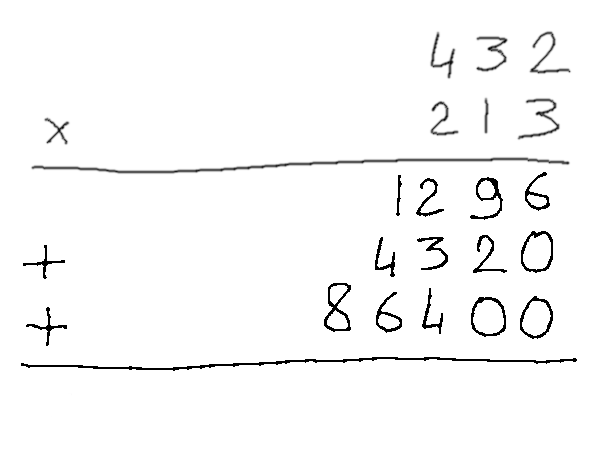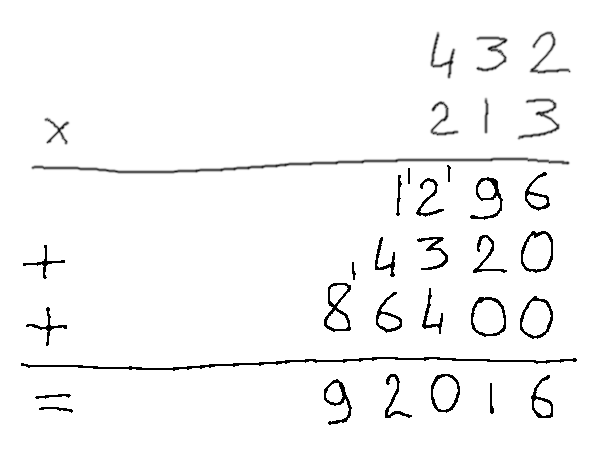
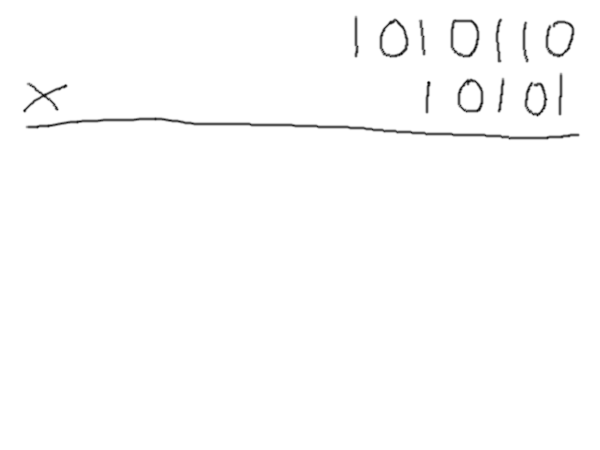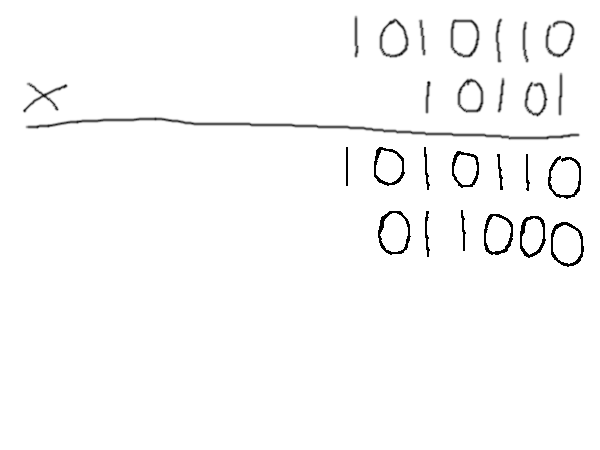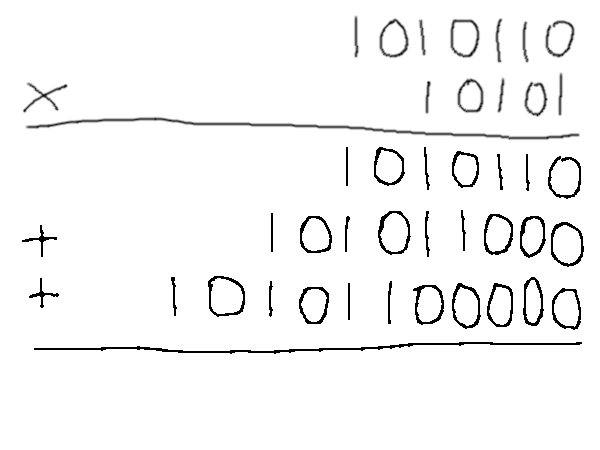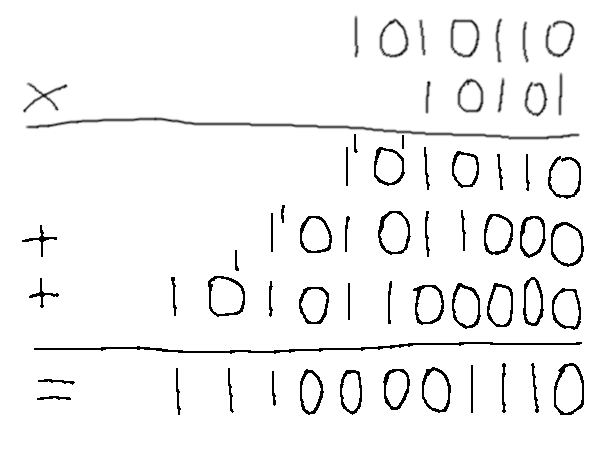
1010/10000 En posant une multiplication « à la main » en binaire, on se rend compte quand même assez vite de quelque chose de plutôt pratique : quand on n'a que des zéros et des uns à manipuler, l'opération devient beaucoup plus simple : multiplier par deux (qui s'écrit « 10 » en binaire) consiste juste à décaler tout d'un cran.

Du coup, n'importe quelle multiplication complexe n'est finalement qu'une suite de décalages et d'additions, ce qui est plutôt simple à faire une fois qu'on a compris la logique. Bon, ça ne nous dit pas forcément combien vaut le résultat exprimé d'une façon plus habituelle, mais on le trouve plus vite quand même.

B/10 Ceci dit, le binaire a ceci de peu pratique pour nous que, s'il n'y a que deux chiffres différents à manipuler, ses nombres se mettent vite à être assez longs, comptant pas mal de fois ces deux chiffres. Les gens qui bossent dans l'informatique ont donc assez vite eu tendance à essayer de regrouper tout ça, par exemple en passant par la base seize, dite « hexadécimal ».

Elle est pratique parce que, seize étant une puissance de deux, on peut passer de l'un à l'autre sans avoir besoin de faire de calculs : un nombre à un seul « chiffre » en hexadécimal correspond à un nombre de quatre chiffres en binaire, de façon complètement transparente.

Je vais m'éviter de trop détailler sur ce point en vous renvoyant à une autre B.D. où @gee explique très bien ça : https://grisebouille.net/hexadecimal-et-boby-lapointe/

14/20 Mais l'hexadécimal n'est pas la seule base « pratique » utilisée en informatique. On utilise aussi parfois l'octal, c'est-à-dire la base huit. Huit aussi est une puissance de deux, donc ça marche aussi bien pour regrouper facilement des nombres binaires. C'est juste un peu moins efficace, puisqu'un nombre d'un chiffre en octal correspond à un nombre de « seulement » trois chiffres en binaire.

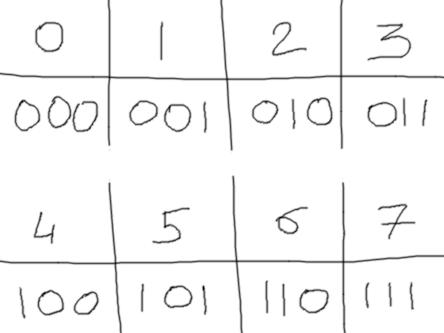
Par exemple, le nombre 20 en décimal va s'écrire 10100 en binaire. Les trois derniers chiffres sont 100, ce qui correspond au nombre 4 (à la fois en octal et en décimal, vu qu'on est en dessous de huit). Les chiffres qui restent forment (0)10, ce qui correspond au chiffre 2 : 20 en décimal va donc s'écrire 24 en octal. À l'inverse, dans le nombre 52 en octal, le 5 s'écrit 101 en binaire, et le 2 s'écrit toujours (0)10, ce qui donne 101010 en binaire, et correspond en décimal à 42.

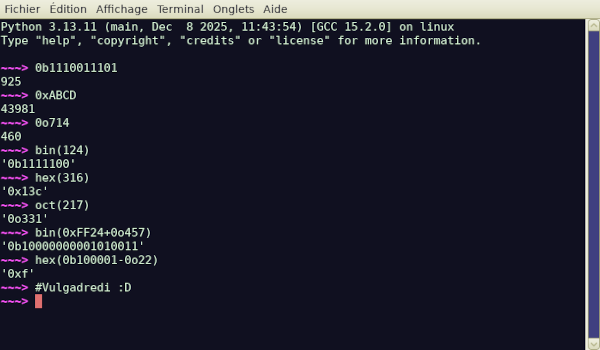
13/16 Vous aurez d'ailleurs remarqué que j'ai converti aussi la numérotation sur les trois derniers pouets. Sans vous prévenir, ce qui rend le truc un peu plus dur à suivre. Histoire de savoir à quoi s'attendre, on a tendance à indiquer quelle base on utilise, quand c'est autre chose que notre base dix usuelle, c'est quand même plus clair.

Ainsi, en informatique, on utilise régulièrement devant les suites de chiffres les préfixes « 0b » pour le binaire, « 0o » pour l'octal et « 0x » pour l'hexadécimal, ce qui permet à la machine de comprendre ça directement. Mais quand on écrit à la main, une autre convention est d'indiquer les trois premières lettres du nom de la base, « bin. », « oct. », « hex. »… ou bien encore « dec. » pour décimal au besoin.

14/16 Et nous en arrivons donc à cette énigme que je vous ai posée à Halloween dernier, et dont la solution doit maintenant vous paraître évidente. Je précise au cas où une nouvelle fois que je la tire d'un des épisodes du Club des Veufs Noirs d'Isaac Asimov, et d'ailleurs j'en profite aussi pour caser un #VendrediLecture, parce que cette série de nouvelles est vraiment très chouette.

Mais donc, dans la nouvelle « un bon père de famille » (« The Family Man » en V.O., deuxième nouvelle du troisième recueil), les Veufs Noirs sont amenés à s'interroger sur un cas tournant autour de l'affirmation selon laquelle « Noël et Halloween, c'est exactement pareil » (il est question d'un type suspect de fraude, mais je vous laisse découvrir les détails en lisant la nouvelle).

16/21 Donc, voilà, notre façon de compter dépend de pas mal de choses et peut varier selon le contexte, mais dans tous les cas, ça reste un truc assez important. D'ailleurs, j'avais consacré un des premiers articles de mon blog⁽*⁾, il y a dix-sept ans, à vous expliquer comment on peut compter sur nos doigts, notamment en allant jusqu'à 12, voire jusqu'à 31, avec une seule main.

Tiens, d'ailleurs, vu que je me suis assez peu autocité dans ce thread, et pour fêter les cinq mois, j'ai envie de rajouter cinq pouets de plus pour vous renvoyer vers quelques autres en particulier, surtout pour les gens qui se sont abonné récemment. Mais si vous avez déjà tout lu, je vous dis à la semaine prochaine pour le dernier #vulgadredi de l'année, et donc joyeux Halloween d'ici-là !

(∗) Celui-ci, qui a quelques bouts en commun avec le présent thread : https://fadrienn.irlnc.org/articles/sciences/comptons_sur_nos_doigts/

17/21 Et donc on va commencer par le tout premier article, mentionné plus haut, où je vous causais donc de si des microbes extraterrestres risquent d'être dangereux pour nous ou pas (spoiler : a priori pas plus que le reste de leur planète). C'était un thread improvisé sur le coup, à l'époque je ne pensais pas forcément que j'en ferai d'autres (d'ailleurs je n'avais même pas encore pensé à mettre des hashtags spécifiques), et pourtant nous voici cinq mois plus tard et je compte bien continuer encore un peu.

Je note aussi que c'est visiblement le thread qui a reçu le plus de réactions jusque là, ce qui est quand même un peu dommage parce que j'aime bien avoir l'impression de ne pas trop parler dans le vide, mais bon, je suis sûr que vous pouvez faire en sorte de battre ce record si vous voulez ^^

Bref, c'est par là : https://fadrienn.irlnc.org/notice/AwGiNCEL9iX8pAJcTw

18/21 Autre thread, le plus court et visiblement celui qui a reçu le moins de réaction. Ce qui est dommage parce que c'est pour moi un des plus intéressants : il cause des mythes autour de la constellation de la Grande Ourse et de ce que ça nous raconte sur l'histoire humaine, rien que ça.

C'est aussi le premier pour lequel j'ai pensé à mettre les deux hashtags qui sont maintenant dans le premier post de chaque thread, et aussi le seul jusque là où je vous ai lié directement un article de recherche (vu que j'en avais un en français et publiquement accessible) plutôt que de vous renvoyer vers Wikipédia ou vers le boulot de vulga d'autres gens.

Si vous voulez jeter un œil, c'est ici : https://fadrienn.irlnc.org/notice/AwjRm0n2lOzYwhdHto

19/21 Après le plus court, voici l'un des plus longs : celui où je commente l'« équation » de Drake et la recherche de vie extraterrestre. Qui est aussi celui, rapidement mentionné plus haut, dans lequel je vous parle des différentes inventions de l'agriculture, parce que, si si, ça peut avoir un rapport (en l'occurrence c'est un point intéressant à regarder pour essayer d'évaluer l'incertitude sur le temps d'apparition d'une civilisation).

En vrai, j'aurais probablement préféré plutôt lier le thread sur les conditions d'habitabilité d'une planète, sauf que j'ai mis des liens en arrière, mais pas de liens en avant, donc le plus récent des deux vous permet de retrouver celui d'avant, mais pas l'inverse. Mais n'hésitez pas à aller lire l'autre aussi, il vaut le coup !

Et donc, c'est par là : https://fadrienn.irlnc.org/notice/AxCLpjrQgQ11SSuqau

20/21 Un autre de mes petits préférés, et le dernier à avoir dépassé les désormais habituels seize pouets (enfin, jusqu'à celui-ci, quoi) : celui sur Cérès et la loi de Bode. Je n'en dis pas plus pour vous laisser découvrir tout ça.

Enfin, si, je vous dit en plus qu'il vous permettra de retrouver aussi le thread sur 3I/ATLAS et les comètes en général, qui est bien cool aussi, et que j'aurais probablement lié ici si je n'avais pas décidé de me limiter à cinq pouets pour ne pas trop spammer, mais bon, même principe, je vous mets le plus récent, et à partir de là vous pouvez remonter.

Donc c'est par ici : https://fadrienn.irlnc.org/notice/AyMztvDdmCsEVRGpYe

21/21 Et donc pour finir, j'avais quand même aussi envie de revenir un peu sur la partie où je causais de biologie, parce qu'il n'y a pas que l'astronomie dans la vie. Et donc je vais choisir le premier thread de la série, celui qui parlait d'évolution et de prédiction scientifique, parce qu'il me semble qu'il y a quelques trucs importants dedans, mais là encore, sur la même logique, je devrais plutôt lier le dernier et vous laisser remonter. Mais bon, je vous ai déjà balancé pas mal de liens, là.

D'ailleurs, je tâcherai peut-être en début d'année prochaine de mettre une page quelque part chez moi pour pouvoir retrouver facilement tous les épisodes du feuilleton (y a déjà un sujet dédié à ça sur la Couronne de Cuivre, si ça vous branche). En attendant, donc, on va s'arrêter là pour cette fois, et je réfléchis à ce dont je vais parler la semaine prochaine. Les suggestions sont les bienvenues, comme d'hab !

Et pour le thread en question : https://fadrienn.irlnc.org/notice/AybcCRXAswcqPg6ZLE