C'est de nouveau #VendrediVulga, et pour le #Vulgadredi de cette semaine, après un petit détour par la biologie, on va donc revenir un peu à l'astronomie. Mais en fait, on va parler finalement un peu du même sujet dans les deux cas, à savoir : arrêtons de nous prendre pour le centre du monde.
Grace, notamment, aux travaux de Darwin et Wallace qu'on a évoqué dans les dernières semaines, on a pu se rendre compte qu'on n'est qu'une espèce ordinaire, apparue par hasard un peu comme toutes les autres, et non pas le sommet de l'évolution. On va maintenant voir que notre planète n'est pas non plus au centre de l'univers, et ça va nous prendre seize pouets, vu que ce format continue de pas trop mal marcher.
Au fait, si vous avez manqué la conclusion de notre escapade biologique, le thread de la semaine dernière est là : https://fadrienn.irlnc.org/notice/AzXXsM9y1i7hIy5lqK
Grace, notamment, aux travaux de Darwin et Wallace qu'on a évoqué dans les dernières semaines, on a pu se rendre compte qu'on n'est qu'une espèce ordinaire, apparue par hasard un peu comme toutes les autres, et non pas le sommet de l'évolution. On va maintenant voir que notre planète n'est pas non plus au centre de l'univers, et ça va nous prendre seize pouets, vu que ce format continue de pas trop mal marcher.
Au fait, si vous avez manqué la conclusion de notre escapade biologique, le thread de la semaine dernière est là : https://fadrienn.irlnc.org/notice/AzXXsM9y1i7hIy5lqK
2/16 Mais commençons par noter qu'arrêter de se prendre pour le centre du monde, c'est peut-être aussi arrêter de prendre nos ancêtres pour des imbéciles. Du haut de notre science moderne, on a parfois un peu tendance à regarder les anciennes générations comme si les gens de l'époque n'avaient cru que des bêtises… comme l'idée saugrenue que le Soleil tournerait autour de la Terre.
Alors, oui, ils ont cru ça, même si en vrai la question a pas mal été discutée et que plusieurs modèles concurrents existaient déjà à l'époque pour expliquer les mouvements du ciel, mais surtout : c'est loin d'être aussi absurde que ça peut nous le sembler aujourd'hui, et pas mal d'entre nous auraient probablement cru ça en disposant des mêmes connaissances qu'à l'époque.
Alors, oui, ils ont cru ça, même si en vrai la question a pas mal été discutée et que plusieurs modèles concurrents existaient déjà à l'époque pour expliquer les mouvements du ciel, mais surtout : c'est loin d'être aussi absurde que ça peut nous le sembler aujourd'hui, et pas mal d'entre nous auraient probablement cru ça en disposant des mêmes connaissances qu'à l'époque.

3/16 Parce que ce qui motivait cette idée, ce n'était pas juste une forme d'égocentrisme nous mettant au centre de tout. L'idée découle de quelques réflexions assez solides sur le monde qui nous entoure. En effet, dans la vie de tous les jours, si on lâche un objet, il tombe. Nous savons, nous, maintenant, que c'est la Terre qui l'attire grâce à la gravité, mais quels autres effets concrets de la gravité constatez-vous dans votre vie de tous les jours ?
À partir de ce qu'on peut empiriquement constater, on peut assez facilement se dire que le haut et le bas sont des directions absolues, qui ne dépendent pas de l'endroit où on se trouve : les objets lourds tombent vers le bas, c'est tout, c'est l'univers qui est comme ça. Or, la Terre sous nos pieds est assez manifestement un objet lourd. Il semble donc cohérent qu'elle doive elle aussi tomber vers le bas.
À partir de ce qu'on peut empiriquement constater, on peut assez facilement se dire que le haut et le bas sont des directions absolues, qui ne dépendent pas de l'endroit où on se trouve : les objets lourds tombent vers le bas, c'est tout, c'est l'univers qui est comme ça. Or, la Terre sous nos pieds est assez manifestement un objet lourd. Il semble donc cohérent qu'elle doive elle aussi tomber vers le bas.

4/16 Et pourtant, nous ne sentons pas vraiment la Terre se déplacer. Pourquoi ne semble-t-elle pas en train de tomber ? Peut-être parce que, depuis le temps, elle a fini par l'atteindre, ce « bas ». Si la Terre, qui a sans doute pu finir sa chute longtemps avant que nous soyons là pour en parler, est déjà posée sur l'endroit qui attire tout le reste, alors il est normal que tout le reste lui tombe dessus dès qu'on le lâche.
Et si les objets célestes (que, sans instrument optique, on ne voit que comme des points lumineux dans le ciel, sans pouvoir dire comment ils sont composés ni à quelle distance ils sont) ne tombent pas, c'est peut-être qu'ils sont constitués d'une autre sorte de matière, différente de la nôtre, qui elle ne tombe pas vers le bas, mais se contente de tourner autour. Ce qui revient à les faire tourner autour de la Terre, mais sans que la Terre elle-même n'ait besoin d'y être pour quoi que ce soit.
Et si les objets célestes (que, sans instrument optique, on ne voit que comme des points lumineux dans le ciel, sans pouvoir dire comment ils sont composés ni à quelle distance ils sont) ne tombent pas, c'est peut-être qu'ils sont constitués d'une autre sorte de matière, différente de la nôtre, qui elle ne tombe pas vers le bas, mais se contente de tourner autour. Ce qui revient à les faire tourner autour de la Terre, mais sans que la Terre elle-même n'ait besoin d'y être pour quoi que ce soit.
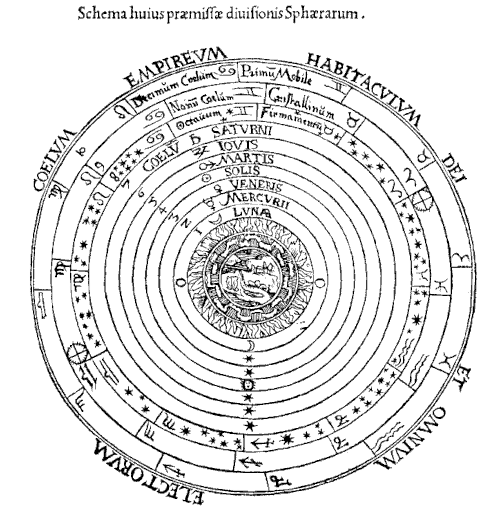
5/16 C'est grosso-modo, sauf erreur de ma part, l'un des raisonnements que tenait Aristote il y a plus de 2300 ans, et compte tenu de ce qu'il avait à sa disposition, c'était plutôt solide et pas mal trouvé. Nous savons maintenant que c'est faux, certes ; mais c'est parce que nous avons empilé pas mal de travaux scientifique depuis cette époque, sans lesquels nous n'aurions sans doute pas fait mieux que lui.
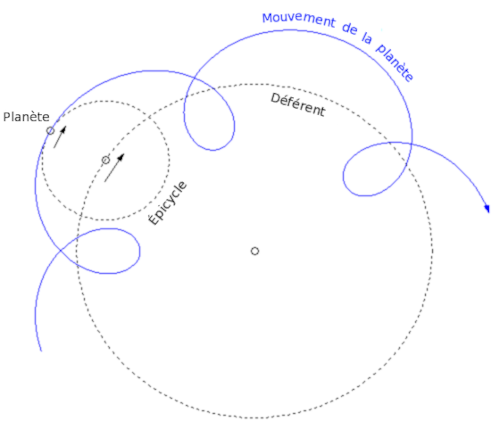
De même, si ses (plus ou moins) contemporains tentent d'expliquer les mouvements des planètes avec uniquement des cercles imbriqués, ce qui donne donc des mouvements un peu compliqués avec des « épicycles », c'est sans doute parce que le cercle était à l'époque considéré comme une forme géométrique parfaite, mais peut-être aussi (je m'avance un peu ici, si un·e spécialiste de l'histoire des maths veut bien confirmer ou infirmer) parce qu'avant de pouvoir se dire que les mouvements des planètes sont des ellipses, il faut déjà avoir une notion solide et utilisable de comment ça marche une ellipse, ce qui n'était peut-être pas encore disponible à l'époque.
De même, si ses (plus ou moins) contemporains tentent d'expliquer les mouvements des planètes avec uniquement des cercles imbriqués, ce qui donne donc des mouvements un peu compliqués avec des « épicycles », c'est sans doute parce que le cercle était à l'époque considéré comme une forme géométrique parfaite, mais peut-être aussi (je m'avance un peu ici, si un·e spécialiste de l'histoire des maths veut bien confirmer ou infirmer) parce qu'avant de pouvoir se dire que les mouvements des planètes sont des ellipses, il faut déjà avoir une notion solide et utilisable de comment ça marche une ellipse, ce qui n'était peut-être pas encore disponible à l'époque.
6/16 Quand, dans sa par ailleurs plutôt chouette vidéo sur Mars, @defakator nous fait le petit sketch où Ptolémée confond les étoiles parce qu'il a besoin de lunettes qui n'existent pas encore, c'est amusant, et ce n'est pas spécialement gênant (et je dis ça pour mettre en avant cette vidéo, mais mes collègues et moi pouvons faire des blagues du même niveau au cours d'une séance de planétarium), mais ça illustre quand même un point de vue assez moqueur sur le passé qui n'est pas forcément si pertinent que ça.
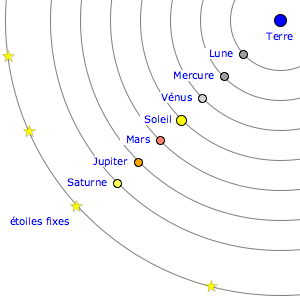
En vérité, le modèle de fonctionnement du ciel que Claude Ptolémée, se basant sur tout un tas de travaux antérieurs, met au point au deuxième siècle, est environ ce qu'on peut faire de plus solide et de plus précis compte tenu des connaissances antiques. C'est un modèle qui met la Terre au centre, certes, mais qui marche fichtrement bien par rapport à ce qu'on peut observer dans notre ciel.
En vérité, le modèle de fonctionnement du ciel que Claude Ptolémée, se basant sur tout un tas de travaux antérieurs, met au point au deuxième siècle, est environ ce qu'on peut faire de plus solide et de plus précis compte tenu des connaissances antiques. C'est un modèle qui met la Terre au centre, certes, mais qui marche fichtrement bien par rapport à ce qu'on peut observer dans notre ciel.
7/16 D'ailleurs, si on finira par remettre en cause ce modèle, ce n'est pas parce qu'on se serait rendu compte qu'il est faux : pour décrire les mouvements des planètes dans le ciel, et prédire à l'avance l'endroit où on va les observer, on peut encore de nos jours utiliser le système de Ptolémée, et ça marche encore très bien. Non, le seul souci de ce modèle, c'est qu'à une époque où on n'avait pas encore de machines pour calculer à notre place, des cercles dans les cercles dans les cercles, ça demandait beaucoup de boulot.
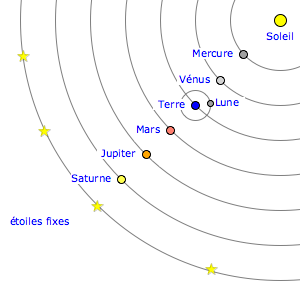
Et c'est donc surtout pour essayer de simplifier les calculs que Mikołaj Kopernik (dit Nicolas Copernic en français) va tenter d'organiser le système différemment, en mettant le Soleil au centre et en faisant tourner la Terre autour, avec les planètes. Et au moment de la publication de ses travaux, son modèle, même s'il était plus « simple » au sens où il demandait un peu moins d'épicycles (il restait basé sur ces cercles parfaits) et donc moins de calculs, était aussi moins précis que le vieux modèle de Ptolémée.
Et c'est donc surtout pour essayer de simplifier les calculs que Mikołaj Kopernik (dit Nicolas Copernic en français) va tenter d'organiser le système différemment, en mettant le Soleil au centre et en faisant tourner la Terre autour, avec les planètes. Et au moment de la publication de ses travaux, son modèle, même s'il était plus « simple » au sens où il demandait un peu moins d'épicycles (il restait basé sur ces cercles parfaits) et donc moins de calculs, était aussi moins précis que le vieux modèle de Ptolémée.
8/16 À l'époque de Copernic, cependant, la situation a pas mal changé par rapport à l'Antiquité. Notamment, l'Église catholique s'est imposée, et a fait beaucoup pour propager l'idée que l'Homme, conçu par Dieu à Son image, se détacherait du reste du monde vivant, et serait au centre de toute chose (certains passages de la Bible parlent du Soleil qui « s'arrêterait dans sa course », ce qui nécessite donc que ce soit lui qui bouge).
Copernic va donc beaucoup hésiter à publier ses travaux, et ce n'est que l'année de sa mort, en 1543, que sera imprimé son ouvrage principal, De Revolutionibus Orbium Coelestium (soit « des révolutions des sphères célestes »). Andreas Osiander, qui supervisa l'impression, prendra d'ailleurs grand soin d'y faire préciser que le but de l'ouvrage était juste de faciliter les calculs, et absolument pas de décrire la façon dont la réalité fonctionnerait.
Copernic va donc beaucoup hésiter à publier ses travaux, et ce n'est que l'année de sa mort, en 1543, que sera imprimé son ouvrage principal, De Revolutionibus Orbium Coelestium (soit « des révolutions des sphères célestes »). Andreas Osiander, qui supervisa l'impression, prendra d'ailleurs grand soin d'y faire préciser que le but de l'ouvrage était juste de faciliter les calculs, et absolument pas de décrire la façon dont la réalité fonctionnerait.

9/16 Néanmoins, malgré cette précaution, l'ouvrage permettra de réouvrir le débat, et plusieurs astronomes de la seconde moitié du seizième siècle et du début du dix-septième se poseront la question : entre la Terre et le Soleil, qui des deux tourne autour de l'autre ? Et la question n'est franchement pas triviale.
Car en effet, comme mentionné plus haut, dans la vie de tous les jours, on ne sent pas la Terre bouger. Et toutes les observations qu'on pouvait faire jusque là pouvaient, au prix de systèmes plus ou moins complexes, être expliqués dans un cas comme dans l'autre. Pour arriver à trancher, il nous faudrait donc une nouvelle observation… ou au contraire, une prédiction théorique, conséquence d'une des deux hypothèses, qu'on n'arriverait pas à observer en pratique.
Car en effet, comme mentionné plus haut, dans la vie de tous les jours, on ne sent pas la Terre bouger. Et toutes les observations qu'on pouvait faire jusque là pouvaient, au prix de systèmes plus ou moins complexes, être expliqués dans un cas comme dans l'autre. Pour arriver à trancher, il nous faudrait donc une nouvelle observation… ou au contraire, une prédiction théorique, conséquence d'une des deux hypothèses, qu'on n'arriverait pas à observer en pratique.

10/16 C'est sur ce dernier point que va travailler Tycho Brahe. Né quelques années après le décès de Copernic, il sera l'un des observateurs du ciel les plus actifs et rigoureux de l'histoire de l'astronomie, ce qui est d'autant plus impressionnant qu'il mourra plusieurs années avant l'invention de la lunette astronomique et effectuera donc tout son travail à l'œil nu. Ayant eu la chance d'observer notamment une supernova et une comète, il remettra en cause à plusieurs reprises les travaux d'Aristote et des autres astronomes antiques.
Pour ce qui nous intéresse ici, il cherchera à trancher la question à partir d'une hypothèse simple : si la Terre tourne autour du Soleil, alors elle doit se déplacer de façon assez importante dans l'espace, et donc avoir un angle de vue légèrement différent. En observant le ciel avec six mois d'écart, au maximum de cette distance, on devrait pouvoir observer des étoiles qui se déplacent les unes par rapport aux autres, par un phénomène qu'on appelle la parallaxe.
Pour ce qui nous intéresse ici, il cherchera à trancher la question à partir d'une hypothèse simple : si la Terre tourne autour du Soleil, alors elle doit se déplacer de façon assez importante dans l'espace, et donc avoir un angle de vue légèrement différent. En observant le ciel avec six mois d'écart, au maximum de cette distance, on devrait pouvoir observer des étoiles qui se déplacent les unes par rapport aux autres, par un phénomène qu'on appelle la parallaxe.
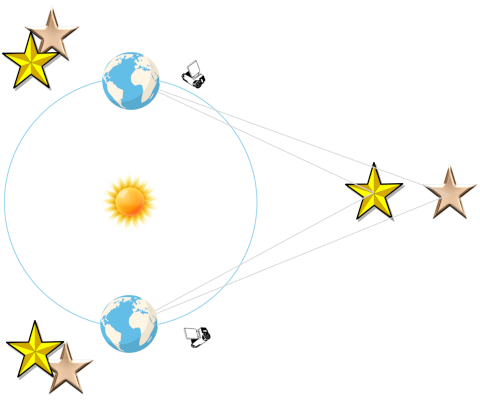
11/16 Le souci ici est que les étoiles sont très lointaines : tellement lointaines que, pour pouvoir observer une telle parallaxe, il est nécessaire de disposer d'un télescope. Friedrich Wilhelm Bessel finira par en mesurer, mais seulement en 1828. À son époque et sans instrument optique, Tycho Brahe sera forcé de conclure qu'il ne trouve pas cette preuve… et donc que la Terre ne bouge probablement pas.
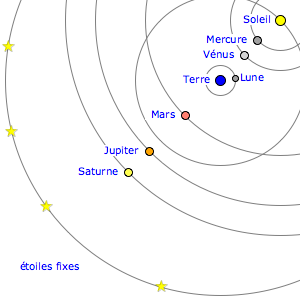
Il est tout de même partiellement convaincu par les travaux de Copernic, et mettra au point une sorte de système hybride, dans lequel le Soleil tourne autour de la Terre, comme l'avançait Ptolémée, puisqu'il semble alors impossible de prouver le contraire, mais dans lequel les (autres) planètes, elles, tournent autour du Soleil selon la proposition de Copernic.
Il est tout de même partiellement convaincu par les travaux de Copernic, et mettra au point une sorte de système hybride, dans lequel le Soleil tourne autour de la Terre, comme l'avançait Ptolémée, puisqu'il semble alors impossible de prouver le contraire, mais dans lequel les (autres) planètes, elles, tournent autour du Soleil selon la proposition de Copernic.
12/16 Tycho Brahe aura néanmoins une autre contribution très utile : il prendra comme assistant un jeune astronome du nom de Johannes Kepler, qui sera chargé de le remplacer à sa mort en 1601. Kepler était pour sa part convaincu que la Terre se déplaçait et que le « bon » modèle était celui de Copernic, et il travaillera à affiner ce modèle, identifiant peu à peu les trois « lois de Kepler » que nous utilisons encore de nos jours.
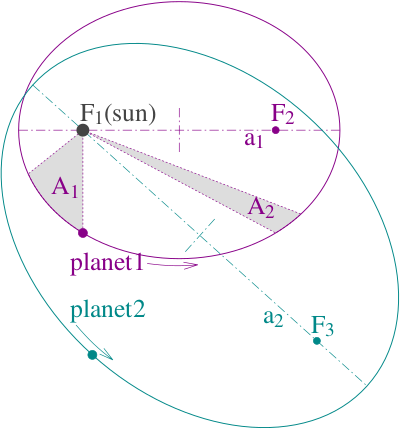
C'est à lui que nous devons l'abandon des cercles parfaits et des épicycles au profit des ellipses, qui décrivent beaucoup mieux les mouvements réels des corps célestes. Cependant, même s'il a rendu le modèle de Copernic plus précis et encore plus simple d'utilisation, Kepler non plus n'a pas réussi à prouver que la Terre se déplace.
C'est à lui que nous devons l'abandon des cercles parfaits et des épicycles au profit des ellipses, qui décrivent beaucoup mieux les mouvements réels des corps célestes. Cependant, même s'il a rendu le modèle de Copernic plus précis et encore plus simple d'utilisation, Kepler non plus n'a pas réussi à prouver que la Terre se déplace.
13/16 Et Galilée, dans tout ça ? Vous savez sans doute qu'il a été un des premiers à observer les corps célestes à la lunette astronomique, vers 1610, et que l'Église lui a fait un procès en 1633. Mais à quel point a-t-il contribué à ce débat ? En fait, pas beaucoup, et plutôt mal.
S'il a contribué très utilement à d'autres progrès des connaissances en physique, son rôle dans la mise en évidence du mouvement de la Terre est beaucoup plus limité. Ses observations (notamment celles des lunes autour de Jupiter) ont été assez utiles, mais pouvaient être expliquées aussi bien dans les autres modèles, donc ça n'a pas prouvé grand chose.
Mais ça, j'en ai déjà parlé en vidéo, alors je vous laisse aller voir ça : https://skeptikon.fr/videos/watch/1071c32c-e50b-4e23-9338-472f3a87a4e5
S'il a contribué très utilement à d'autres progrès des connaissances en physique, son rôle dans la mise en évidence du mouvement de la Terre est beaucoup plus limité. Ses observations (notamment celles des lunes autour de Jupiter) ont été assez utiles, mais pouvaient être expliquées aussi bien dans les autres modèles, donc ça n'a pas prouvé grand chose.
Mais ça, j'en ai déjà parlé en vidéo, alors je vous laisse aller voir ça : https://skeptikon.fr/videos/watch/1071c32c-e50b-4e23-9338-472f3a87a4e5
- replies
- 1
- announces
- 0
- likes
- 0
14/16 Le modèle de Copernic revu et corrigé par Kepler est devenu de plus en plus populaire au fil du dix-septième siècle, et la plupart des astronomes de l'époque ont fini par s'y rallier. Mais, pendant longtemps, le modèle de Brahe, sinon celui de Ptolémée, restai(en)t tout aussi défendable(s). Comment a-t-on fini par trancher ? En découvrant un autre phénomène optique, jusqu'alors inconnu.
Ce phénomène, baptisé « aberration », fait qu'un observateur en mouvement rapide va voir les objets avec un angle légèrement différent de celui que va constater un observateur immobile. Cette différence est encore minime à la vitesse à laquelle la Terre se déplace, mais elle ne dépend pas de la distance à laquelle se trouve l'objet observé, et se trouve donc être légèrement plus prononcée que celle due à la parallaxe évoquée plus haut.
Mais pour plus de détails, je vous renvoie à la page Wikipédia dédiée : https://fr.wikipedia.org/wiki/Aberration_de_la_lumi%C3%A8re
Ce phénomène, baptisé « aberration », fait qu'un observateur en mouvement rapide va voir les objets avec un angle légèrement différent de celui que va constater un observateur immobile. Cette différence est encore minime à la vitesse à laquelle la Terre se déplace, mais elle ne dépend pas de la distance à laquelle se trouve l'objet observé, et se trouve donc être légèrement plus prononcée que celle due à la parallaxe évoquée plus haut.
Mais pour plus de détails, je vous renvoie à la page Wikipédia dédiée : https://fr.wikipedia.org/wiki/Aberration_de_la_lumi%C3%A8re
15/16 Ce phénomène d'aberration n'est pas non plus visible à l'œil nu, mais l'amélioration des moyens optiques réalisée depuis l'invention de la lunette astronomique a fini par permettre de le remarquer, puis de le comprendre, en 1727… soit l'année de la mort d'Isaac Newton, bien après que celui-ci, se basant entre autres sur les travaux de Kepler, nous ait fourni sa théorie de la gravitation universelle.
Il s'est donc écoulé quasiment deux siècles entre la proposition de Copernic de placer le Soleil, plutôt que la Terre, au centre du système, et la première véritable confirmation expérimentale de cette proposition. Entre temps, de grands progrès techniques comme théoriques ont été réalisés, mais ce qui a joué est surtout un changement de point de vue, conduisant les scientifiques de l'époque à collectivement choisir une hypothèse plutôt qu'une autre sans pouvoir encore trancher.
Il s'est donc écoulé quasiment deux siècles entre la proposition de Copernic de placer le Soleil, plutôt que la Terre, au centre du système, et la première véritable confirmation expérimentale de cette proposition. Entre temps, de grands progrès techniques comme théoriques ont été réalisés, mais ce qui a joué est surtout un changement de point de vue, conduisant les scientifiques de l'époque à collectivement choisir une hypothèse plutôt qu'une autre sans pouvoir encore trancher.

16/16 Ce passage du géocentrisme à l'héliocentrisme sera, au vingtième siècle, le grand exemple à partir duquel l'historien des sciences Thomas Kuhn, dans son ouvrage « La Structure des révolutions scientifiques », définira la notion de paradigmes, et montrera que les facteurs sociaux sont une partie importante de la dynamique des sciences. Mais ce sera une histoire pour une autre fois.
En attendant, et à moins que vous n'ayez d'autres sujets à me suggérer d'ici-là, on tâchera la semaine prochaine de soigner un peu nos égos (ou pas) en parlant de quelque chose qui nous remettra au centre du monde connu : la notion d'univers observable, et avec elle une petite échelle des distances.
D'ici-là, joyeux Noël, et si vous ne voyez pas pourquoi je vous dit ça aujourd'hui, c'est qu'il vous reste une énigme à résoudre : https://fadrienn.irlnc.org/notice/AzhbBBDVBAkEJM0o76
En attendant, et à moins que vous n'ayez d'autres sujets à me suggérer d'ici-là, on tâchera la semaine prochaine de soigner un peu nos égos (ou pas) en parlant de quelque chose qui nous remettra au centre du monde connu : la notion d'univers observable, et avec elle une petite échelle des distances.
D'ici-là, joyeux Noël, et si vous ne voyez pas pourquoi je vous dit ça aujourd'hui, c'est qu'il vous reste une énigme à résoudre : https://fadrienn.irlnc.org/notice/AzhbBBDVBAkEJM0o76
@elzen j'avoue que j'ai eu du mal à comprendre l'explication de l'aberration de la lumière de wikipedia et que cet article m'a davantage mis sur la voie :
https://astronoo.com/fr/articles/aberration-de-la-lumiere.html
@Atoto C'est vrai que l'article de Wikipédia n'est pas tip-top en l'état… et que celui-ci a l'air pas mal du tout à vue de nez, merci pour la trouvaille ! :-)