Le Livre d'Argent

Vous avez sans doute entendu parler d'un certain Isaac Newton. Si vous avez eu l'occasion de lire la Rubrique-à-brac, ce que je vous conseille vivement, vous avez peut-être même en tête l'image de ce type qui s'est prit, selon Gotlib, à peu près tout et n'importe quoi sur la tête.

Eh bien, ça tombe bien, parce que même s'il a apporté sa contribution aux sciences dans de nombreux domaines, notamment via ses Principia Mathematica ou ses travaux sur l'optique (qui ont sans doute contribué à l'élaboration de mon convertisseur de longueurs d'ondes), c'est de cette histoire de pomme (ou de zèbre, de pélican…) que je veux vous parler aujourd'hui.

Isaac Newton, donc, après avoir reçu un violent choc à la tête résultant de la chute d'un objet quelconque, s'est trouvé dans l'état de divagation adéquat pour formuler une loi d'attraction universelle, stipulant que la matière attire la matière, et quelle équation régissait cette attraction.

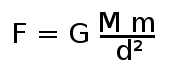
La valeur de l'attraction s'exerçant entre deux corps, selon Newton, est égale au produit des masses des deux corps divisé par le carré de la distance les séparant, le tout multiplié par une constante dont il n'a cependant pas pris la peine de chercher à déterminer la valeur. Fin de l'histoire.

…de celle de Newton, en tout cas, pour ce qui nous intéresse aujourd'hui. Car passé ce rappel du contexte, c'est plutôt à un autre scientifique que nous allons nous intéresser pour l'instant. Sir Henry Cavendish était tout aussi anglais que son prédécesseur et a vécu peu de temps après lui. Et entre autres travaux scientifiques, ce brave homme s'est mis en tête de déterminer la masse de la planète sur laquelle sont posés nos pieds (du moins pour les moins tête-en-l'air d'entre nous).

Le raisonnement de Cavendish était le suivant : d'après la formule sus-citée laissée par son collègue, si l'on connaît la force d'attraction qui s'exerce entre deux corps, la distance les séparant, la masse d'un de ces deux corps et cette fameuse constante que Newton n'a pas déterminé, retrouver la masse du second corps revient à résoudre une équation tout ce qu'il y a de plus simple. Mathématiquement parlant, c'est un jeu d'enfant.

Or, la distance entre un objet quelconque et le centre de l'attraction terrestre correspond à peu de choses près au rayon de la Terre, puisque ce centre d'attraction est également le centre de notre planète. Cette distance nous est connue depuis un bon moment puisqu'un certain Ératosthène en avait déjà déterminé une estimation quelques deux mille cent ans plus tôt si je calcule bien (Je vous ferai peut-être un autre texte pour vous expliquer comment il s'y est pris, un de ces jours).

Déterminer la masse précise de l'objet quelconque en question ne posait pas trop de problème non plus, à condition peut-être de choisir l'objet adéquat. Quant à la valeur de la force d'attraction exercée par la Terre sur cet objet, sa mesure est tellement simple que certains d'entre vous la prennent peut-être tous les jours en montant sur leur balance: même si l'aiguille vous indique une masse en (kilo)grammes, ce que mesure réellement un instrument tel que votre pèse-personne est en réalité votre poids, c'est-à-dire la force exercée sur vous par la Terre, et qui s'exprime, en l'honneur du découvreur de la formule, en Newton.

Si l'on pouvait connaître cette fameuse constante, on disposerait de tous les paramètres requis pour déterminer la masse de notre bonne vieille terre. Ce qui serait une bonne idée, ne trouvez-vous pas ? Pour parvenir à son but, Sir Cavendish devait donc entreprendre de déterminer cette constante. Comment faire ? Eh bien, en appliquant le même raisonnement dans le sens inverse, tout simplement.

En connaissant cette fois précisément la distance séparant deux objets, la masse de chacun de ces deux objets et la force qui s'exerce entre eux, déterminer la constante ne devrait poser aucun problème. La distance, c'était aisément mesurable. La masse, il suffisait de bien choisir les objets. La difficulté expérimentale était de déterminer la force d'attraction s'exerçant entre deux objets suffisamment petits pour que l'on puisse les manipuler. Et Sir Cavendish avait justement une idée de la manière de procéder.

Pour cela, il a décidé de se doter, en premier lieu, d'un pendule de torsion, comme celui de la photo ci-dessus (trouvée sur Wikipédia), et de deux boules de plombs de trente centimètres de diamètre, qu'il place chacune d'un côté du fléau. L'ensemble mesure deux mètres, et comme notre scientifique tient à éliminer le plus possible les risques de perturbations, il fait maçonner autour de son modèle, qui se trouve donc isolé à l'intérieur d'une sorte de bâtiment sans porte ni fenêtres. Pour lire tout de même le résultat de l'expérience, il perce un trou dans l'axe du fléau, et laisse le tout reposer trois jours pour que tous les courants d'airs se calment et que les boules de plomb attirent convenablement le fléau.

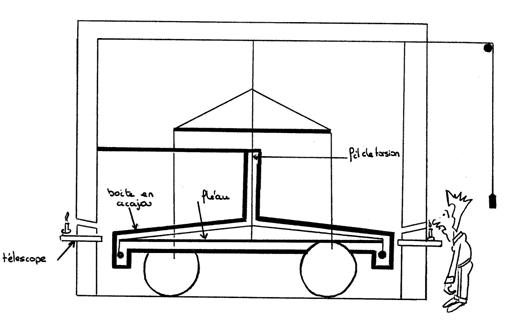
Il regarde ensuite par ce trou, et note l'angle de décalage entre son trou et le fléau, celui-ci s'étant décalé en direction des grosses masses de plomb. Sir Cavendish actionne alors un mécanisme qui va modifier la position des boules, afin d'inverser leur attraction. De cette manière, le fléau va tourner dans l'autre sens, et l'angle entre ses positions aux deux observations va permettre de déterminer la force s'exerçant sur le fléau. Vu de dessus :

Ce décalage va doubler le déplacement effectué, permettant donc de mieux le repérer. Il suffit ensuite de diviser le résultat obtenu par deux, et d'en tirer par calcul la valeur de la force. Après avoir effectué cette expérience, Sir Cavendish trouve une valeur pour la constante G de 6,754×10⁻¹¹, et son calcul lui indique donc, pour notre planète Terre, une masse de 5,980×10²⁴.

Sachant qu'avec tous nos outils actuels, nous trouvons respectivement 6,674×10⁻¹¹ et 5,974×10²⁴, on peut quand même lui tirer notre chapeau, non ? Et le plus impressionnant, c'est que même si les conditions expérimentales se sont améliorées depuis (en particulier, la précision accrue des outils de mesure nous permet de prendre un fléau beaucoup plus petit et donc nettement moins sensible aux variations extérieures), c'est toujours ce même principe expérimental que l'on utilise de nos jours pour calculer cette constante gravitationnelle.

(Je tiens à remercier mon professeur de Sciences Physiques au Lycée puis à l'IUFM, qui a brillamment expliqué ce principe, démonstration par l'expérience à l'appui, lors d'une conférence au Palais de la Découverte)