Le Livre d'Argent

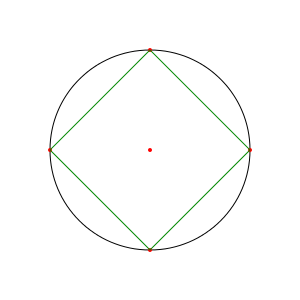
Je vous propose une jolie énigme de construction mathématiques qu'un camarade (Grünt, pour ne pas le nommer) m'a posée il y a quelques temps.

Le principe est assez simple : il s'agit de trouver les quatre sommets d'un carré inscrit dans un cercle. La difficulté est qu'il faut y parvenir en utilisant uniquement le compas (oui, vous avez bien lu : pas de règle, même non-graduée).

En fait, cela peut se faire en moins d'une dizaine d'étapes. Pour débuter, c'est assez simple : choisissez un point, qui servira de centre, tracez un cercle de la taille qui vous plaira, puis prenez n'importe quel point du cercle, qui sera le premier sommet de votre carré. Un peu comme ça :

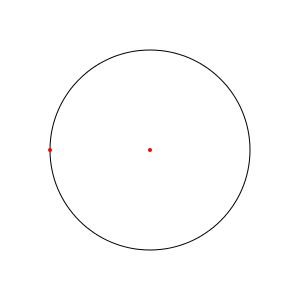
Maintenant, si vous voulez chercher par vous-mêmes, arrêtez simplement ici la lecture de cet article, et vous reviendrez quand vous voudrez lire ma solution. Si vous préférez enchaîner directement, sans chercher… eh bien, ce serait dommage, me semble-t-il, mais c'est vous que ça regarde

La première étape, pour résoudre notre petit problème, est de prendre votre premier sommet, et de tracer un second cercle, qui passerait par le centre du premier. En fait, vous n'êtes pas obligés de tracer le cercle complet ; mais comme on s'en re-servira un peu plus tard, ça vaut peut-être mieux.

Pour la lisibilité du schéma, j'ai un peu tronqué le mien :

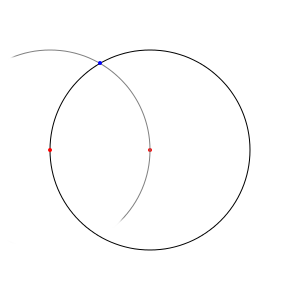
Les deux cercles dont nous disposons maintenant ont deux intersections. L'une d'entre elle nous sera utile, l'autre pas. Je vous laisse décider laquelle des deux vous préférez (je l'ai, sur la figure, notée en bleu, et non pas en rouge comme les deux points précédents, parce qu'il s'agit d'un simple point de construction ; c'est pour différencier des points qui nous intéressent vraiment).

En prenant ce troisième point comme centre, on peut tracer un troisième cercle qui passera encore par le centre du premier. Inutile de tracer ce cercle en entier, cependant : la seule chose qui nous intéresse vraiment, c'est l'intersection suivante.

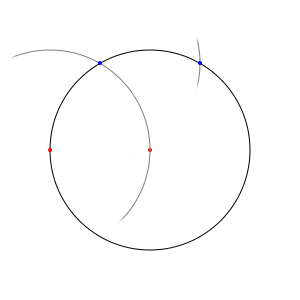
Et la raison pour laquelle cette intersection nous intéresse, c'est qu'en répétant encore une fois la même opération (tracer, en la prenant comme centre, un cercle qui passe par notre point de départ), nous obtenons le point du cercle d'origine qui est diamétralement opposé au premier sommet de notre carré… qui est donc lui-même un point de notre carré, puisque les diagonales d'un carré inscrit dans un cercle dont des diamètres de ce cercle.

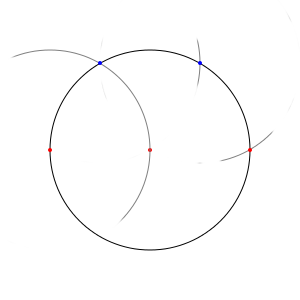
Si nous répétions encore cette opération, nous pourrions facilement arriver à tracer un hexagone régulier inscrit dans notre cercle. Mais c'est un carré, que nous voulons, et pas un hexagone, en tout cas pour cette fois. Continuons donc.

La question est maintenant de savoir comment on peut, en utilisant le compas seul, trouver un deuxième diamètre du cercle qui soit perpendiculaire au premier.

Trouver un point quelconque (c'est-à-dire : n'importe lequel, sauf celui qu'on cherche ^^) d'une droite perpendiculaire à une autre, c'est assez simple. Piquez la pointe du compas dans l'un de nos deux sommets, écartez le compas de façon à atteindre le point intermédiaire de l'autre côté, et tracez un premier arc de cercle ; puis recommencez l'opération dans l'autre sens, et les deux arcs de cercles, si vous avez bien visé, se croiseront quelque part sur la droite que vous cherchez.

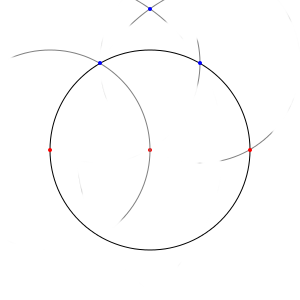
…le problème, c'est que ce n'est pas au bon endroit, puisque vous ne touchez pas à notre cercle d'origine. Mais ce point nous sera utile quand même. En effet, en remettant la pointe de votre compas sur le centre du cercle d'origine, vous pouvez tracer un nouveau cercle qui contiendra le premier. Et vous trouvez alors une intersection entre ce nouveau cercle et celui que nous avions tracé au début :

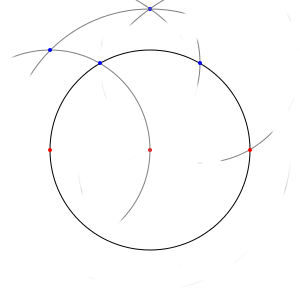
Or, il se trouve que ce point, par construction, est situé à égale distance entre notre premier sommet, et l'un des deux que nous recherchons encore. Un simple coup de compas nous permettra donc d'obtenir le troisième sommet du carré.

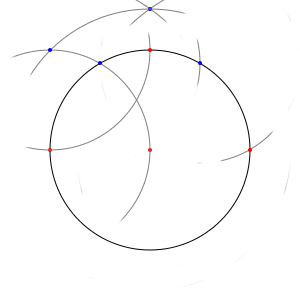
Et une fois que nous en avons trois, trouver le quatrième devient assez simple : il nous sera donné par la seconde intersection entre le centre d'origine et un cercle prenant l'un des sommets du carré comme centre, et de rayon le côté du carré.

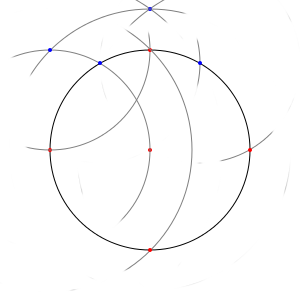
Une fois arrivé là, vous disposez des quatre sommets recherchés. Il ne vous reste plus qu'à, si vous le désirez, sortir enfin la règle pour tracer plus explicitement notre carré.

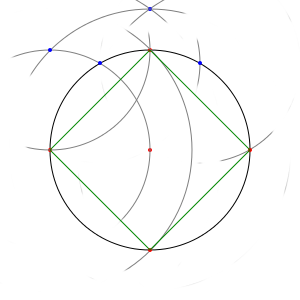
Bien sûr, ce ne serait pas un vrai jeu mathématique si l'on se contentait de considérer que ça marche, comme ça, sans vérifier. Il faut démontrer que cette construction est correcte.

Je dois avouer avoir un peu eu la flemme de le faire moi-même ; mais en cherchant un peu, j'ai trouvé une page intéressante ici (elle s'attaque à un problème différent, mais qui a quelques points communs avec le nôtre. En fait, c'est en jetant un œil à la figure au bout de ce lien que j'ai trouvé comment finir ma construction).

Si ça vous intéresse, voici un fichier SVG que j'ai constitué à ce sujet : il m'a servi de base pour générer les images ci-dessus ; et j'ai indiqué, assez rapidement, les différentes étapes de constructions dans les commentaires qu'il contient (ouvrez-le avec un éditeur de texte pour jeter un œil à son code source, c'est du fait-main, donc assez simple).

Une petite remarque supplémentaire, au sujet de ce qui précède : cette rapide explication vous aura peut-être, au passage, fait prendre conscience de la raison pour laquelle on jongle avec autant de lettres dans les exercices de géométrie habituels : appeler l'un des points « A » et le suivant « B » facilite beaucoup les explications, en vous permettant de situer plus facilement celui qu'il faut utiliser parmi tous ceux que nous avons sur la figure.