§ Posté le 18/11/2013 à 2h 09m 00
Je vous avais, il y a un bon moment de ça(1), expliqué le concept de bases, et comment on pouvait compter sur ses doigts en base douze et en binaire. Et je vous avais indiqué, au passage, que le binaire est la « langue » dans laquelle parlent nos ordinateurs. Puisque nos ordinateurs comptent ainsi, il est intéressant que les humains qui créent des programmes pour les ordinateurs sachent un peu comment ça marche, histoire de faire attention à certains petits détails.
Mes étudiants doivent donc apprendre à compter en binaire, et je me suis dit qu'un petit article à ce sujet pourrait vous intéresser vous aussi (donc désolé rushou, tu n'apprendras rien sur mon blog cette fois-ci).
Vous savez déjà que, en base deux, écrire un nombre prend une certaine place. Par exemple, 14 s'écrit 1110, et 18 s'écrit 10010. Je vous avais donc expliqué, en note, que l'on pouvait utiliser l'octal (base 8) et l'hexadécimal (base 16) pour écrire ça en plus condensé.
En effet, huit et seize sont des puissances de deux : 8 = 2³ et 16 = 2⁴. Cela signifie que tous les nombres entre zéro et sept s'écrivent en trois chiffres binaires, et occupent toutes les combinaisons de trois chiffres binaires possibles : de 000 à 111. On a donc une correspondance directe entre trois chiffres binaires et un seul chiffre octal, sans qu'il y ait de perte d'information. De même, quatre chiffres binaires donnent un unique chiffre hexadécimal. Avec notre base dix usuelle, qui n'est pas une puissance de deux, ça ne peut pas marcher, puisque huit et neuf dépassent des trois chiffres, sans pour autant remplir toutes les combinaisons en utilisant un quatrième.
Cependant, si on favorise les bases huit et seize pour gagner de la place, le binaire apporte certaines facilités au niveau des calculs. Pour voir cela, je vais remettre un bref instant ma casquette de professeur des écoles, et vous rappeler comment nous posions les opérations à l'école élémentaire. Commençons par une addition : 152 + 181.
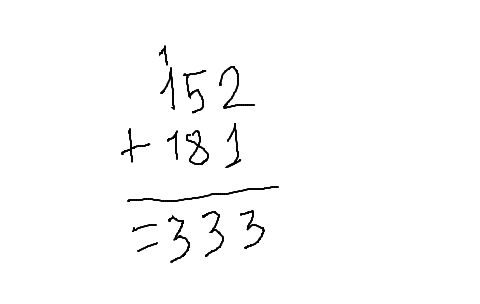
L'image ci-dessus vous rappellera sans doute quelque chose : on écrit les deux nombres l'un en dessous de l'autre, et on procède chiffre par chiffre, en commençant par les unités. 2 + 1 = 3, aucun soucis, on écrit trois sur la ligne de résultat, et on passe aux dizaines. Là, 5 + 8 = 13. Puisqu'on ne veut qu'un seul chiffre, on ne note que le 3, et on reporte le 1 sur la colonne d'à côté (ce que l'on appelle une « retenue »), ce qui nous donne donc 1 + 1 + 1 = 3, et nous obtenons 333 comme résultat.
En binaire, nous allons procéder exactement de la même façon, à cette différence près que, comme on n'a pas de chiffres plus grands que un, on procède avec beaucoup de retenues. Un exemple, avec 110101 + 011010.
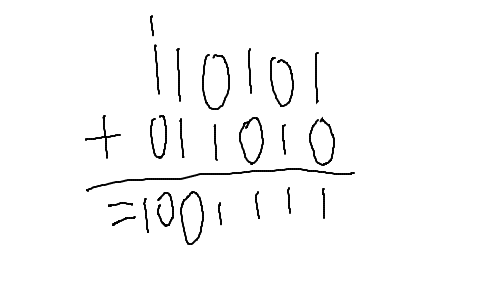
Pour les quatre premiers chiffres (toujours en partant de la droite), on n'a aucun soucis : 1 + 0 ou 0 + 1 donnent 1. Quand on arrive au chiffre suivant, 1 + 1 donne 10. On écrit donc le zéro, et l'on garde le 1 pour la colonne d'à côté. 1 + 0 + 1 donne encore 10, donc on recommence, et le résultat s'écrit donc 1001111. Je vous laisse calculer combien ça fait en décimal pour vérifier si vous le désirez, mais voyez que l'on a pu faire l'opération directement en binaire.
Un petit problème que l'on peut rencontrer ici, quand on est dans une machine, est que le résultat peut facilement avoir quelques chiffres de plus que nos deux nombres de départ. Si l'on code un nombre sur un octet, soit huit chiffres binaires(2), on peut donc facilement arriver à un « débordement » faisant qu'on perd de l'information (on y arrive précisément quand on atteint 2⁸ = 256).
En pratique, je vous rassure, on utilise plusieurs octets pour coder un seul entier, et on a donc une limite largement plus importante, mais le concept reste là, et utiliser des très grands nombres nécessite des réglages particuliers.
Passons maintenant aux soustractions. Le principe est très exactement le même, mais commençons cette fois encore par une soustraction en base dix : 129 - 76.
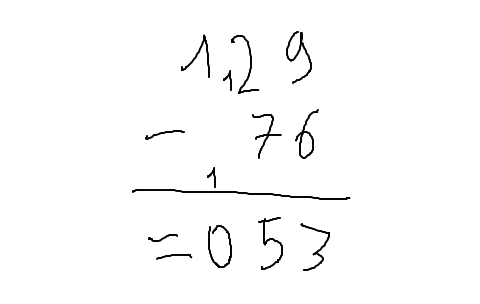
9 - 6 donnent 3, facile, on l'écrit. 2 - 7, ça va être plus dur (je vous rappelle qu'à l'époque où vous avez appris à faire ça, vous ne connaissiez pas encore les nombres négatifs). On va donc encore une fois utiliser une retenue, mais cette fois-ci, dans l'autre sens : on prend une « dizaine » un peu plus loin, et on calcule donc 12 - 7 = 5, et on la reporte à l'étape suivante, qui devient donc : 1 - 0 - 1 = 0. Nous obtenons donc 53.
C'est bon, vous voyez ? Alors essayons avec une soustraction en binaire : 101101 - 010101.
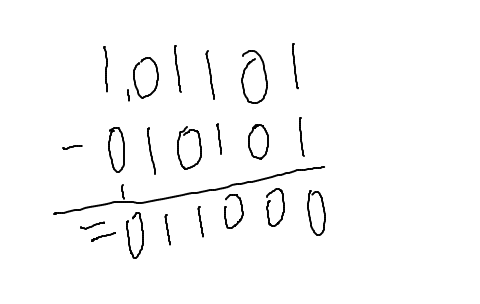
Pour les trois premiers (toujours en partant de la droite) chiffres, identité parfaite entre le haut et le bas, le résultat est donc zéro. Le chiffre suivant (ou précédent, si vous préférez), 1 - 0 = 1, aucune difficulté. Pour le suivant, 0 - 1 pose un peu soucis, donc on fait 10 - 1 = 1, et on retranche la retenue au chiffre suivant : 1 - 0 - 1 = 0. Nous obtenons donc 011000.
Passons maintenant aux multiplications. Nous connaissions les tables par cœur, mais poser de plus grosses opérations commençait à devenir un peu plus compliqué, n'est-ce pas ? Essayons avec 326 × 212.
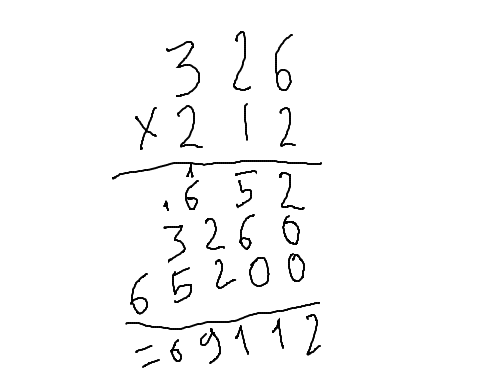
Nous commencions, souvenez-vous, par multiplier 326 par 2 (le chiffre des unités), ce qui nous donnait 652 (ça va, multiplier par deux, on y arrive encore de tête). Puis, le chiffre des dizaines étant 1, on multipliait par 10. Multiplier par 10, c'est facile, il suffit de tout décaler d'un cran vers la gauche (et ajouter un zéro au bout pour boucher le trou créé). Ça nous fait donc 3260. Pour les centaines, on doit donc multiplier par 200, donc à la fois décaler de deux rangs vers la gauche, et multiplier par deux : 65200. Pour obtenir le résultat, il suffit ensuite d'additionner nos trois nombres : 652 + 3260 + 65200 = 69112 (on retombe sur une addition posée, comme plus haut).
La bonne nouvelle, c'est qu'en binaire, nous n'avons que des 0 et des 1 : ça veut dire qu'il n'y aura pas d'opérations compliquées, n'est-ce pas ? En effet, nous n'aurons, comme pour les dizaines ci-dessus, qu'à effectuer les décalages requis et à additionner ensuite. Voyons ça avec 10110101 × 110.
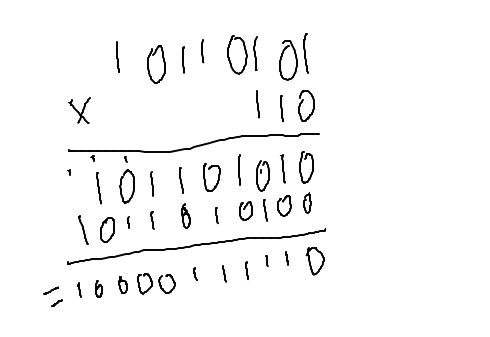
Pour les unités, on multiplie par zéro, donc ça donne zéro, et on peut zapper cette ligne. Pour la suivante, on multiplie par 10, ce qui signifie qu'il suffit de décaler d'un cran, comme on l'aurait fait en base dix. Ça nous donne donc 101101010. Ensuite, on multiplie par 100, ce qui nous donne donc 1011010100. Il suffit d'additionner ces deux nombres, pour obtenir 10000111110.
Voici donc une des raisons pour lesquelles nos machines calculent vite : en binaire, une multiplication se résume à une série de décalages et d'additions, opérations largement plus simples.
Et pour les divisions ? Si vous devez diviser par une puissance de deux, ça va être facile : comme en décimal avec les puissances de dix, il suffira de faire un décalage dans l'autre sens, donc cette fois vers la droite. On peut cependant faire des divisions un peu plus avancées, en les posant, comme nous le faisions à l'école élémentaire.
Comme à l'école élémentaire, nous nous en tiendrons ici aux divisions euclidiennes, c'est-à-dire que nous resterons à des nombres entiers, et que nous aurons donc éventuellement un reste à nos divisions. Essayons, pour l'exemple décimal, avec 148 ÷ 3.
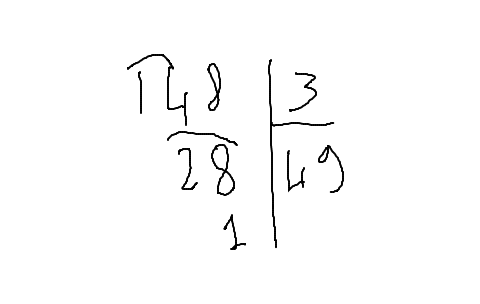
On commence par prendre autant de chiffres, sur la gauche de notre dividende, qu'il nous en faut pour pouvoir caser notre diviseur (si ces deux mots vous semblent mystérieux, vous pouvez retourner lire cet article). Ici, 1 ne suffisant pas, nous devons prendre 14. Nous cherchons alors, en 14, combien de fois on peut caser 3. En l'occurrence, quatre fois, et il nous reste 2. Nous écrivons ce 2, et nous allons ensuite chercher le chiffre suivant, et nous nous demandons maintenant combien de fois on peut caser 3 dans 28 : il y va neuf fois, et il reste 1. Nous n'avons alors plus de chiffres à aller chercher, et nous pouvons donc nous arrêter là : 148 ÷ 3 donne 49, et il reste 1.
On essaye avec des nombres binaires ? Ça devrait rester à notre portée. Essayons 110110 ÷ 101.
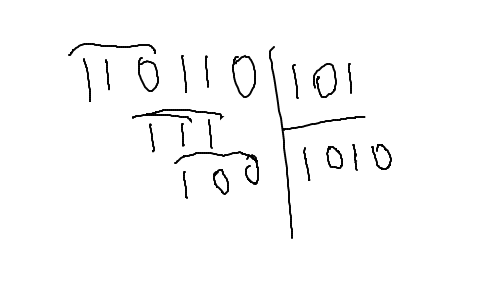
Pour réussir à caser 101, il nous faut aller chercher les trois premiers chiffres. Combien de fois pouvons-nous mettre 101 dans 110 ? Une seule, à première vue, ce qui est tout à fait normal, puisque notre résultat ne doit compter que des zéros et des uns. Il nous restera 110 - 101 = 1. Si nous abaissons un seul chiffre, 101 ne rentrera pas : nous notons donc 0, et nous abaissons le chiffre suivant. En 111, 101 rentre une fois, et il nous reste maintenant 10. Il nous reste un dernier chiffre, mais 100 est trop petit pour y caser 101, donc nous écrivons encore une fois 0, et nous pouvons donc dire que 110110 divisé par 101 donne 1010, et qu'il reste 100.
Facile, non ?
Bon, pour ceux qui ont trouvé ça trop simple, allons un peu plus loin avec l'algèbre de Boole, du nom du mathématicien qui a formalisé ça. Les informaticiens font référence à son nom à chaque fois qu'ils utilisent des « booléens », c'est-à-dire des variables ne pouvant prendre que les valeurs « vrai » et « faux ».
En effet, l'algèbre de Boole ne fonctionne qu'avec deux nombres : 0 et 1. Notez que j'ai bien dit nombres, et non pas chiffres : je rappelle que les chiffres sont aux nombres ce que les lettres sont aux mots. Nous n'aurons donc ici que zéro (ou faux) et un (ou vrai), et pas deux, ni trois, ni la suite, quelle que soit la façon dont on l'écrive.
Dans une telle situation, nos opérations habituelles marchent un peu moins bien que d'habitude. En fait, nous utilisons ici quatre opérateurs particuliers : non, et, ou et ou exclusif (respectivement not, and, or, xor pour nos amis anglophones).
Voyons ça de plus près : « non A », que l'on note ¬A, signifie que, quelle que soit la valeur de A, on prend l'autre valeur. Ainsi, ¬1 = 0 et ¬0 = 1.
A et B, vous connaissez : cela signifie que le résultat ne sera vrai que si A et B sont tous deux vrai. En d'autres termes, 0⋅0 = 0, 1⋅0 = 0, 0⋅1 = 0, 1⋅1 = 1. Ça ressemble à nos multiplications habituelles (mais on note aussi A∧B).
Un peu plus compliqué, le ou. Il est inclusif, c'est-à-dire que le résultat de A ou B sera vrai si au moins l'un de nos deux termes est vrai : 0+0 = 0, 1+0 = 1, 0+1 = 1, et, moins habituel, 1+1 = 1 (mais on note aussi A∨B).
Pour le ou exclusif, moins fréquent, les choses sont similaires, à ceci près que quand A et B sont vrais tous deux, le résultat est faux.
Une blague classique, avec ce genre d'opérateurs, est celui de l'informaticienne enceinte, à qui l'on demande si elle attend un garçon ou une fille, et qui répond « vrai ». Mais l'algèbre de Boole sert aussi à des cas plus sérieux, notamment toutes les expressions conditionnelles que l'on utilise habituellement en programmation. N'hésitez donc pas à vous entraîner à manipuler tout ça, ça pourra toujours vous servir 
On peut aussi, bien sûr, faire plein d'autres choses avec des zéros et des uns. Notamment, coder des nombres négatifs, des nombres à virgule, ou même des caractères n'ayant rien à voir avec des nombres (le texte de cet article, par exemple, est arrivé dans votre navigateur sous la forme d'une suite de zéros et de uns). Mais n'en rajoutons pas trop à la fois, je parlerai de ça plus tard si ça vous intéresse.
